The Circumference of WHAT, though - Shane's Database

Inevitable, conversations begin with... "What!? You don't subscribe to the theory that 2000 years ago some dude assumed parallel light rays (against every observation) made a measurement of the angle of the sun, made a comparison to a known distance between two cities, then used the angle of the second observation to conclude THE WHOLE WORLD IS TILTED D AT 23.4 Degrees? Since light beams from the sun that appear crepuscular are simply a trick that make it appear as if they aren't parallel. 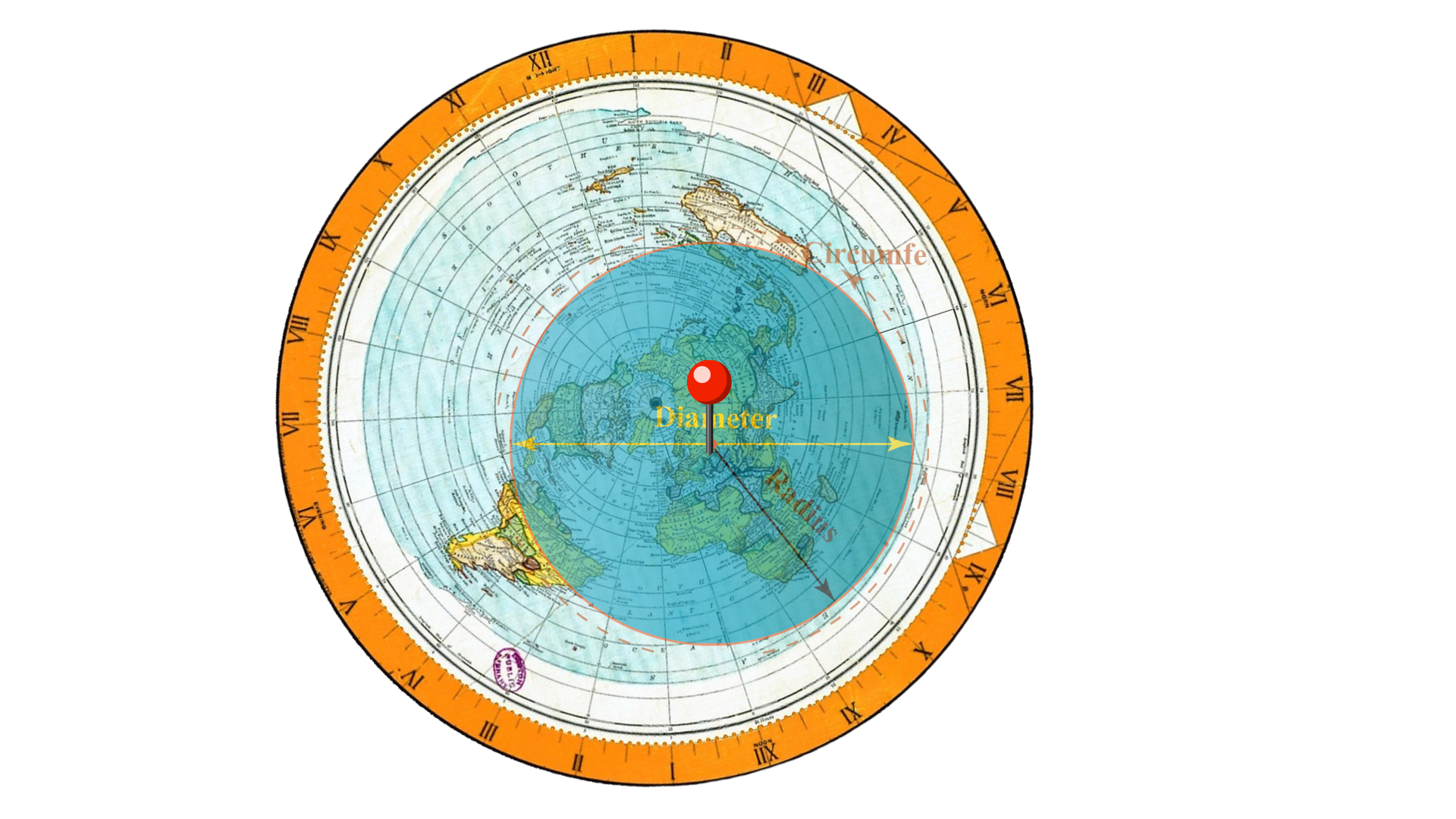Text version of eratosthones https://x.com/AntiDisinfo86/status/1796672034656682111 what actually happened was someone measured the CIRCUMFERENCE of our VISIBLE RADIUS. And told everyone with zero evidence that this applied to the physical globe earth that we stood on.... when it would be optically identical in either case. This circumference is all that has EVER been measured, but the real question is, THE CIRCUMFERENCE OF WHAT? The physically curving ground that you have never seen and has never been measured by any human, ever. period. OR.... The naturally curving celestial hemisphere? Which, again, residents of both models agree is inherently curved, and both treat it as such. It seems the circumference of the circle gets repeatedly measured, but how, in any of these instances, could you differentiate it being the circumference of a planar circle inside a sphere, or the circumference of the visible radius around you into the celestial heaven the same amount in every direction? [Which is also supported by Angular Resolution limit/aperture/wavelength of light/ diameter arguments for an optically curving planar earth] one from the other from inside?? (See animation below) What about that measured angle of the light would be different in a spherically curving earth, or an optically curving planar one? Well there goes the whole basis for the globe ! 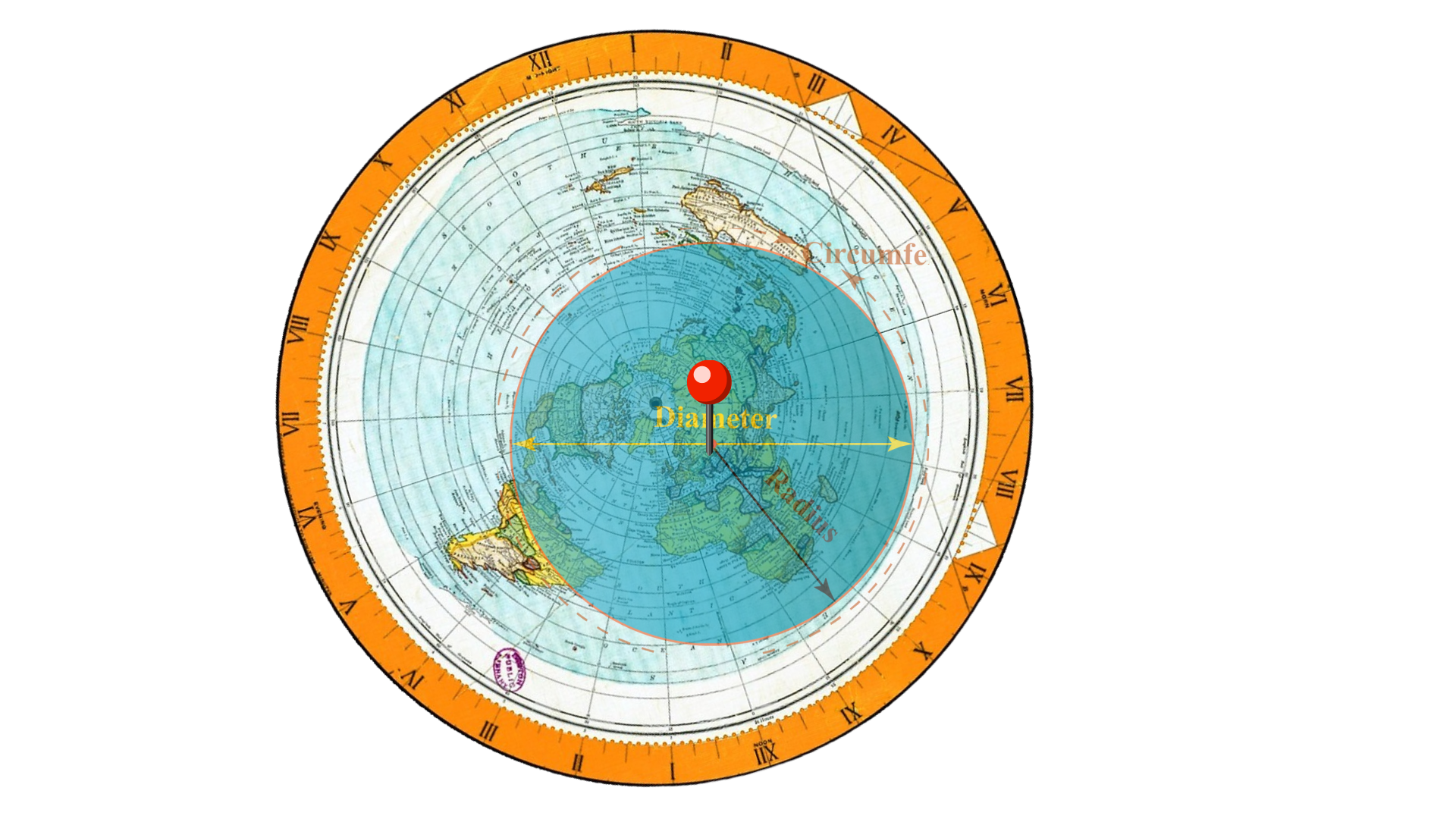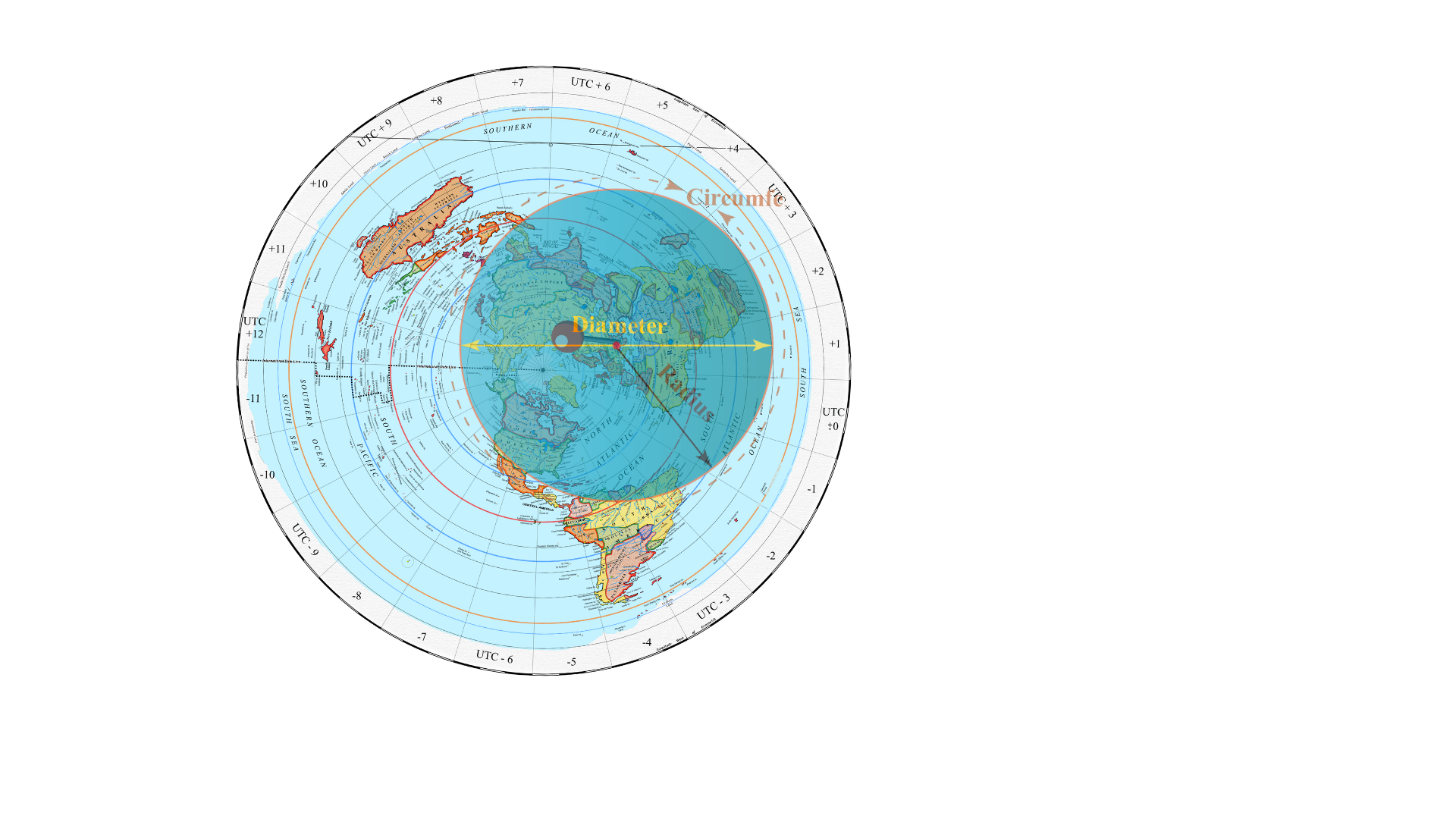![[Attachments/Gleesossdn Map.png]] ![[Attachments/Flat Eassrth Maps.png]] ![[Attachments/51 (4).png]] ![[Attachments/50 (2).png]] ![[Attachments/49 (3).png]] ![[Attachments/53 (3).png]] ![[Attachments/52 (3).png]] Globers: Using just the supposed measurements of Eratosthenes and no coordinate system, please substantiate that these measurement prove the earth is a sphere, more than proving the limits of the sun as denoted on this map. The angular difference in sunlight 7.2 degrees Distance between Syene and Alexandria: 800 km Standing in Alexandria, a circle around the observer with a radius of 3959 matches the exact limits of the sun as observed from there. Otherwise, the evidence of Eratosthenes, more supports a flat earth than a globe earth. 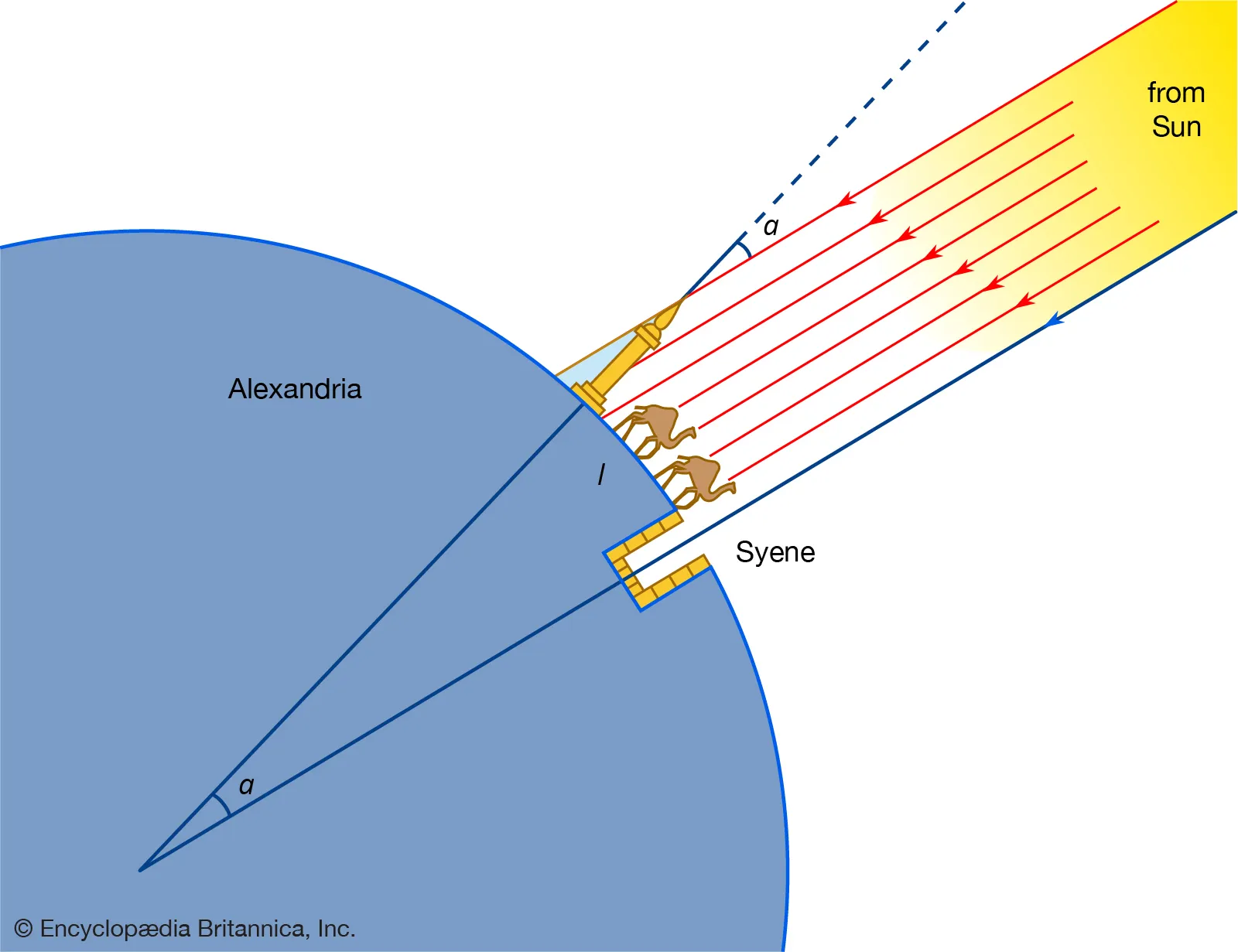https://x.com/AntiDisinfo86/status/1807982947112267789 Eratosthenes, a Greek astronomer, and mathematician, measured the circumference of the Earth around the 3rd century BC. His method involved measuring the angle of the sun's rays at two different locations at the same time. Here's a step-by-step explanation: 1. 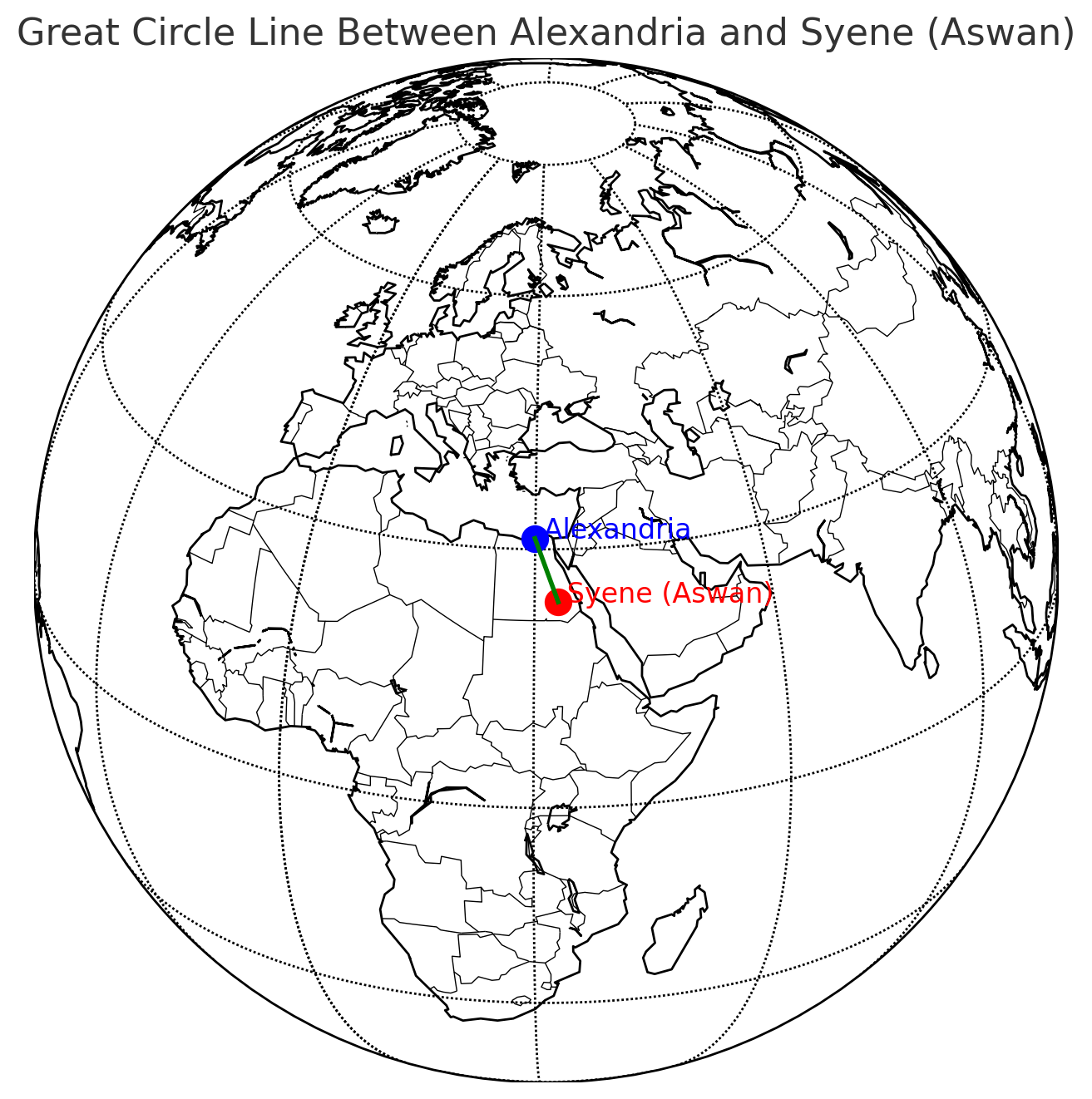**Understanding the Setup:** - Eratosthenes used two cities: Alexandria and Syene (modern-day Aswan), which are approximately 800 km apart. - He observed that at noon on the summer solstice in Syene, the sun was directly overhead (no shadow cast), while in Alexandria, it cast a shadow, indicating the sun was at an angle. 2. 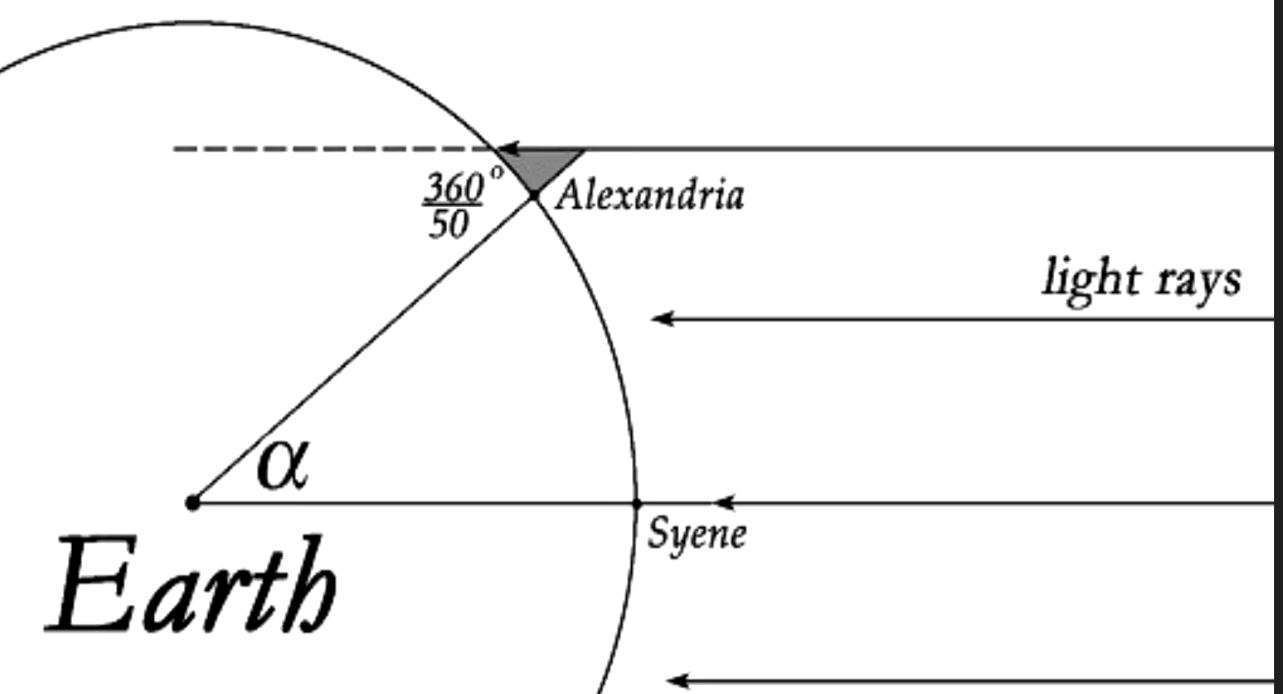**Measurement of the Angle:** - In Alexandria, he measured the angle of the shadow, which was 7.2 degrees. This angle is the central angle corresponding to the arc of the Earth's surface between the two cities. 3. **Calculating the Fraction of the Earth's Circumference:** - The 7.2 degrees is 1/50th of a full circle (since 360 degrees / 7.2 degrees = 50). - This means the distance between Alexandria and Syene (800 km) represents 1/50th of the Earth's total circumference. 4. **Quantifying the Circumference:** - To find the total circumference (C) of the Earth, we use the formula: C=Distance×360∘AngleC = \text{Distance} \times \frac{360^\circ}{\text{Angle}}C=Distance×Angle360∘ - Plugging in the values: C=800 km×360∘7.2∘C = 800 \text{ km} \times \frac{360^\circ}{7.2^\circ}C=800 km×7.2∘360∘ - Simplifying the fraction: C=800 km×50=40,000 kmC = 800 \text{ km} \times 50 = 40,000 \text{ km}C=800 km×50=40,000 km ### Summary Eratosthenes' measurement was based on the following principles: - The difference in the sun's angle (7.2 degrees) between two locations. - The known distance between the two locations (800 km). - Using the proportion of the angle to the full circle (360 degrees) to determine the Earth's circumference. His method provided an estimate for the Earth's circumference that was remarkably accurate for the time, giving a value of approximately 40,000 km. This of course applies to a circle as well as a sphere, especially defined by an that equation calculates the radius of a circle based on the angular resolution and the distance to the horizon. R = d / tan(θ) Where: R = Radius of your spherical vision limit d = Distance to Horizon θ = Angular Resolution Limit Eratosthenes used the cities of Syene (modern-day Aswan) and Alexandria in his famous calculation of Earth's circumference. Here are a few other city pairs and distances that could work similarly for measuring the Earth's circumference using a similar method: ### City Pairs and Distances 1. **Los Angeles and San Francisco, USA** - Approximate Distance: 615 km (382 miles) - Both cities lie roughly on the same longitude. 2. **Cairo, Egypt and Alexandria, Egypt** - Approximate Distance: 180 km (112 miles) - Both cities are on a similar longitude and relatively close, making measurements easier. 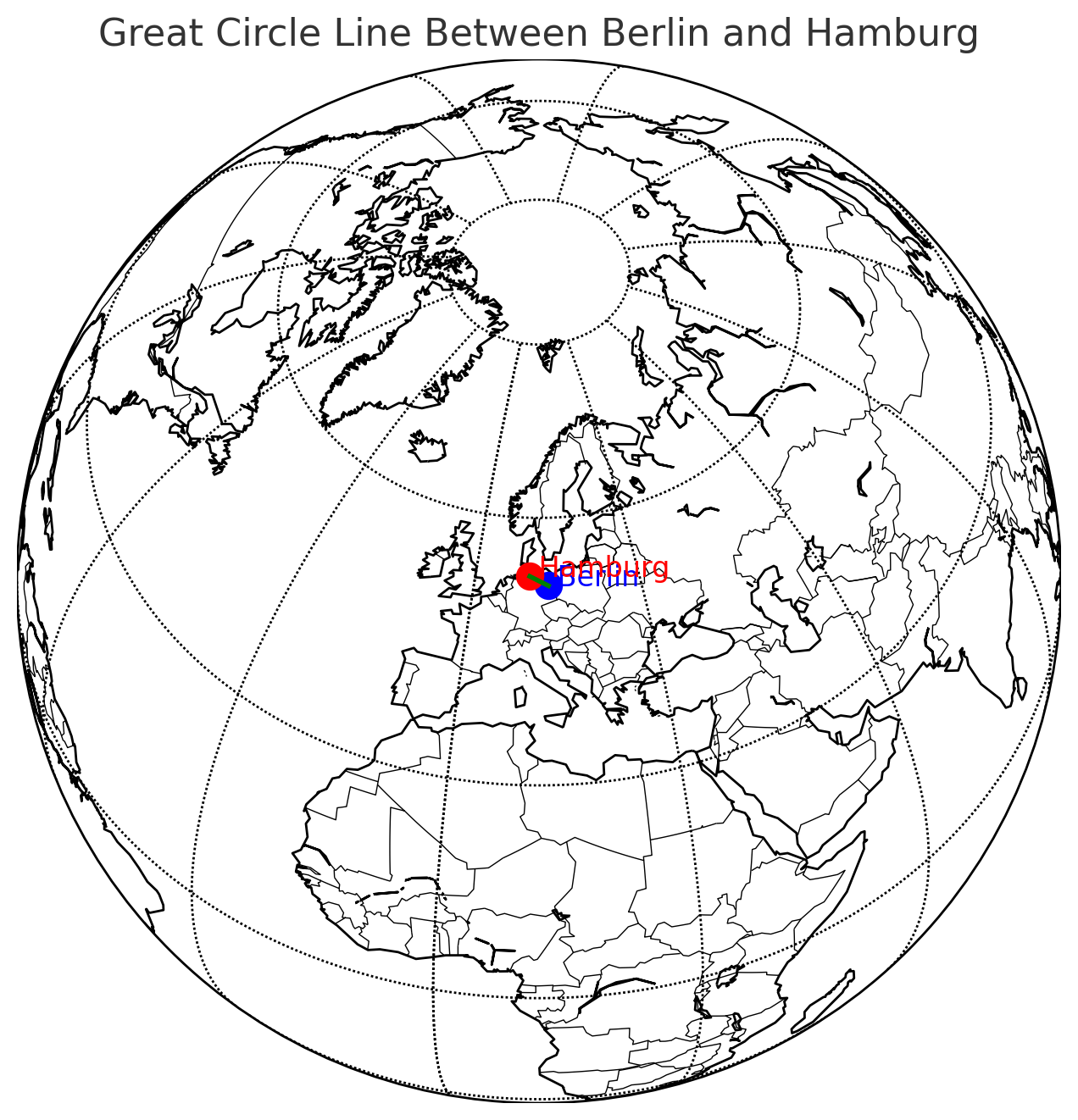3. **Berlin, Germany and Hamburg, Germany** - Approximate Distance: 290 km (180 miles) - Both cities are relatively close and on a similar longitude. 4. **New York City, USA and Washington D.C., USA** - Approximate Distance: 330 km (205 miles) - These cities are relatively close and roughly aligned north-south. 5. **Beijing, China and Tianjin, China** - Approximate Distance: 120 km (75 miles) - Both cities are on a similar longitude and relatively close. 6. **Tokyo, Japan and Yokohama, Japan** - Approximate Distance: 30 km (19 miles) - Both cities are very close and aligned north-south. 7. **Madrid, Spain and Valencia, Spain** - Approximate Distance: 350 km (217 miles) - These cities are relatively close and roughly aligned north-south. 8. **Sydney, Australia and Newcastle, Australia** - Approximate Distance: 160 km (99 miles) - Both cities are on a similar longitude and relatively close. ### Considerations - **Longitude Alignment**: The cities should be on approximately the same longitude (north-south alignment) for the method to work correctly. - **Distance**: The distance between the two cities should be significant enough to measure the angle difference but not so far that it introduces complications due to the curvature of the Earth. - **Measurement Method**: The method relies on the difference in shadow lengths at the two locations at the same time, ideally when the sun is at its highest point. These city pairs provide a range of options for applying a similar method to Eratosthenes' for determining the circumference of the Earth. To calculate the angular size of the sun, we'll use the formula for angular diameter: \[ \theta = 2 \arctan\left(\frac{d}{2D}\right) \] where: - $\theta$ is the angular diameter. - $d$ is the diameter of the sun. - $D$ is the distance from the sun to the Earth. For simplicity, we can approximate $\theta$ using the small angle formula: \[ \theta \approx \frac{d}{D} \] Given: - The diameter of the sun ($d$) is approximately 1,391,000 km. - The average distance from the Earth to the sun ($D$) is approximately 149,600,000 km. Plugging in the values: \[ \theta \approx \frac{1,391,000}{149,600,000} \] \[ \theta \approx 0.0093 \text{ radians} \] To convert radians to degrees: \[ \theta \approx 0.0093 \times \left(\frac{180}{\pi}\right) \] \[ \theta \approx 0.53 \text{ degrees} \] So, the angular size of the sun as seen from Earth is approximately 0.53 degrees. ### Applying the Same Method as Eratosthenes To calculate Earth's circumference using the method of Eratosthenes, you need to know the distance between two locations and the difference in the angle of the sun's rays at those two locations. 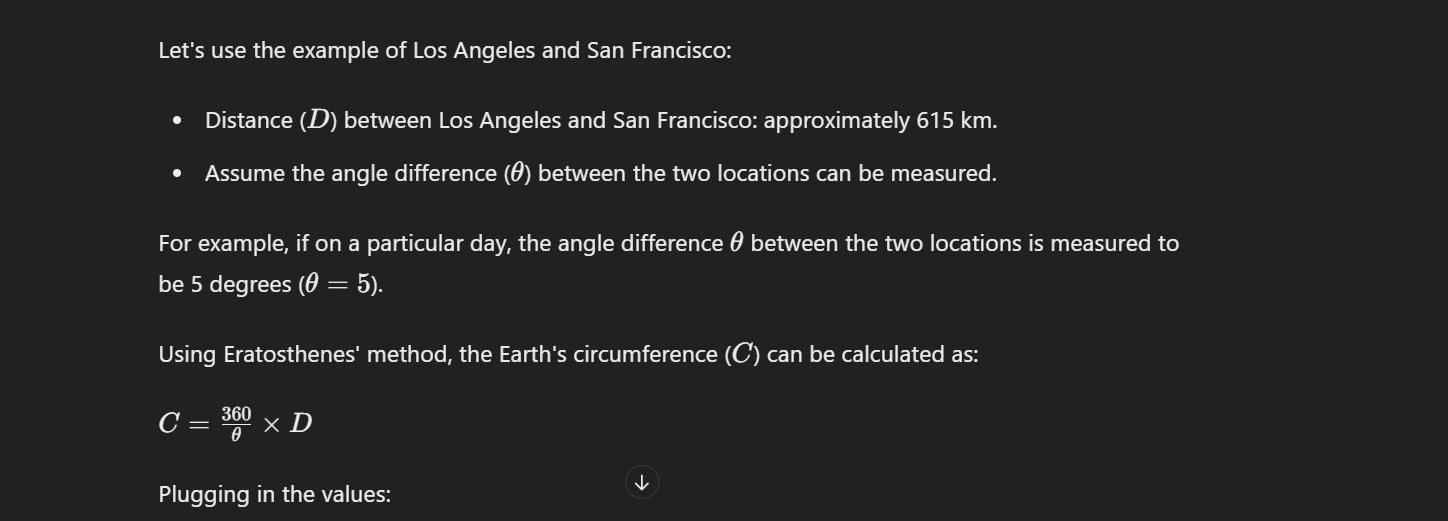Let's use the example of Los Angeles and San Francisco: - Distance ($D$) between Los Angeles and San Francisco: approximately 615 km. - Assume the angle difference ($\theta$) between the two locations can be measured. For example, if on a particular day, the angle difference $\theta$ between the two locations is measured to be 5 degrees ($\theta = 5$). Using Eratosthenes' method, the Earth's circumference ($C$) can be calculated as: \[ C = \frac{360}{\theta} \times D \] Plugging in the values: \[ C = \frac{360}{5} \times 615 \] \[ C = 72 \times 615 \] \[ C = 44,280 \text{ km} \] This is a simplified example. The actual measurement would involve precise measurement of the shadow angles at both locations at the same local time. The calculated circumference may vary depending on the precision of the angle measurement. Using the same method with any pair of cities would involve similar calculations, using the specific distance between the chosen cities and the measured angle difference. ![[Attachments/Pasted image 20240605203042.png]] ![[Attachments/Pasted image 20240605203052.png]] ![[Attachments/Pasted image 20240605203119.png]] ![[Attachments/Pasted image 20240605203212.png]] ![[Attachments/Pasted image 20240626172748.png]] ![[Attachments/Pasted image 20240626172756.png]] ![[Attachments/Pasted image 20240626172745.png]] ![[Attachments/Gleesossdn Map 1.png]] ![[Attachments/Eratosthenes_measure_of_Earth_circumference.svg.png]] ![[Attachments/20secanima-ezgif.com-speed (2).gif]] ![[Attachments/3 (4).png]] ![[Attachments/2 (4).png]] ![[Attachments/2 (4) 1.png]] ![[Attachments/Pasted image 20240628214214.png]] ![[Attachments/Pasted image 20240605203319.png]] ![[Attachments/Pasted image 20240605203328.png]] ![[Attachments/Pasted image 20240605203508.png]] ![[Attachments/Pasted image 20240605203522.png]] Other stuff about the same: Eratosthenes https://www.youtube.com/watch?v=E-YBmX5a3qM&t=3702s How do we know the Circumference of the limit of our vision? https://www.youtube.com/watch?v=94xP53vbPQs&t=4s DEBATISM X Ep X11: Roohif vs. Shane St. Pierre | Curvature: Optical or Physical?https://www.youtube.com/watch?v=VKgcMOhzNO4&t=3s https://www.youtube.com/watch?v=2qz2yJWvvxc&t=49s Circumference of the Spherical Limit of your view What did he measure? https://www.youtube.com/watch?v=9RShOAFh8JE The Truth about Cryptosthenes, Eratosthenes, and the circumference... of what? https://www.youtube.com/watch?v=DY72Op537nk ### How Eratosthenes Measured the Earth's Circumference --- **Narrator:** In the 3rd century BCE, the Greek mathematician Eratosthenes made a groundbreaking calculation that demonstrated the Earth's spherical shape and provided an estimate of its circumference. Here's how he did it. **[Visual: Ancient Greek setting, with Eratosthenes observing the sky]** **Narrator:** Eratosthenes was the head of the Library of Alexandria. He knew that in Syene (modern-day Aswan, Egypt), the Sun was directly overhead at noon on the summer solstice. At the same time in Alexandria, approximately 800 kilometers north, the Sun cast a shadow, indicating it was not directly overhead. **[Visual: Diagram showing the Sun’s rays and the two cities]** ![[Attachments/2 (4) 2.png]] **Narrator:** Eratosthenes measured the angle of the shadow in Alexandria, which was 7.2 degrees. This angle is 1/50th of a full circle (360 degrees). **[Visual: Calculations on a scroll]** ![[Attachments/1 (2) 1.png]] ![[Attachments/Pasted image 20240605203748.png]] ![[Attachments/Pasted image 20240605203838.png]] ![[Attachments/Pasted image 20240605203754.png]] **Narrator:** Using the formula for a circle’s circumference, he reasoned that if 7.2 degrees corresponded to the 800 kilometers between Alexandria and Syene, then 360 degrees would correspond to the entire circumference of the Earth. **[Visual: Mathematical formula appearing on screen]** **Narrator:** He set up a proportion: 7.2360=800 k $Circumference\frac{7.2}{360} = \frac{800 \text{ km}}{\text{Circumference}}3607.2$=Circumference 800 km Solving for the Earth's circumference, he multiplied 800 by 50 (since 360 divided by 7.2 equals 50). **[Visual: Calculation being completed]** **Narrator:** This gave him an estimated circumference of 40,000 kilometers, remarkably close to modern measurements. ![[Attachments/3 (4) 1.png]] ![[Attachments/2 (4) 3.png]] ![[Attachments/eratosthenes method for determining the size of the earth - the same holds true however, if the sun were only 3100 miles away and 34 miles across.jpg]] ![[Attachments/eratosthenes_moon_a_nasa_hoax.jpg]] ![[Attachments/eratosthenes1.jpg]] ![[Attachments/eratosthenes.jpg]] ![[Attachments/Animotica_5_6_6_42_41-ezgif.com-speed.gif]] ![[Attachments/10secani-ezgif.com-video-to-gif-converter.gif]] ![[Attachments/3 (5).png]] ![[Attachments/GNl3JXDWUAEWojk.jpg]] ![[Attachments/GNl3Py5W4AAn1Qr.jpg]] ![[Attachments/GNl4DI4WAAAyN1R.jpg]] ![[Attachments/GNl28Z3WgAA3rQ3.jpg]] ![[Attachments/GNljD46XQAA3Xqo.jpg]] ![[Attachments/GNlqFU8XEAIZwDB (1).jpg]] ![[Attachments/GNlwW5_XMAABdEV.jpg]]