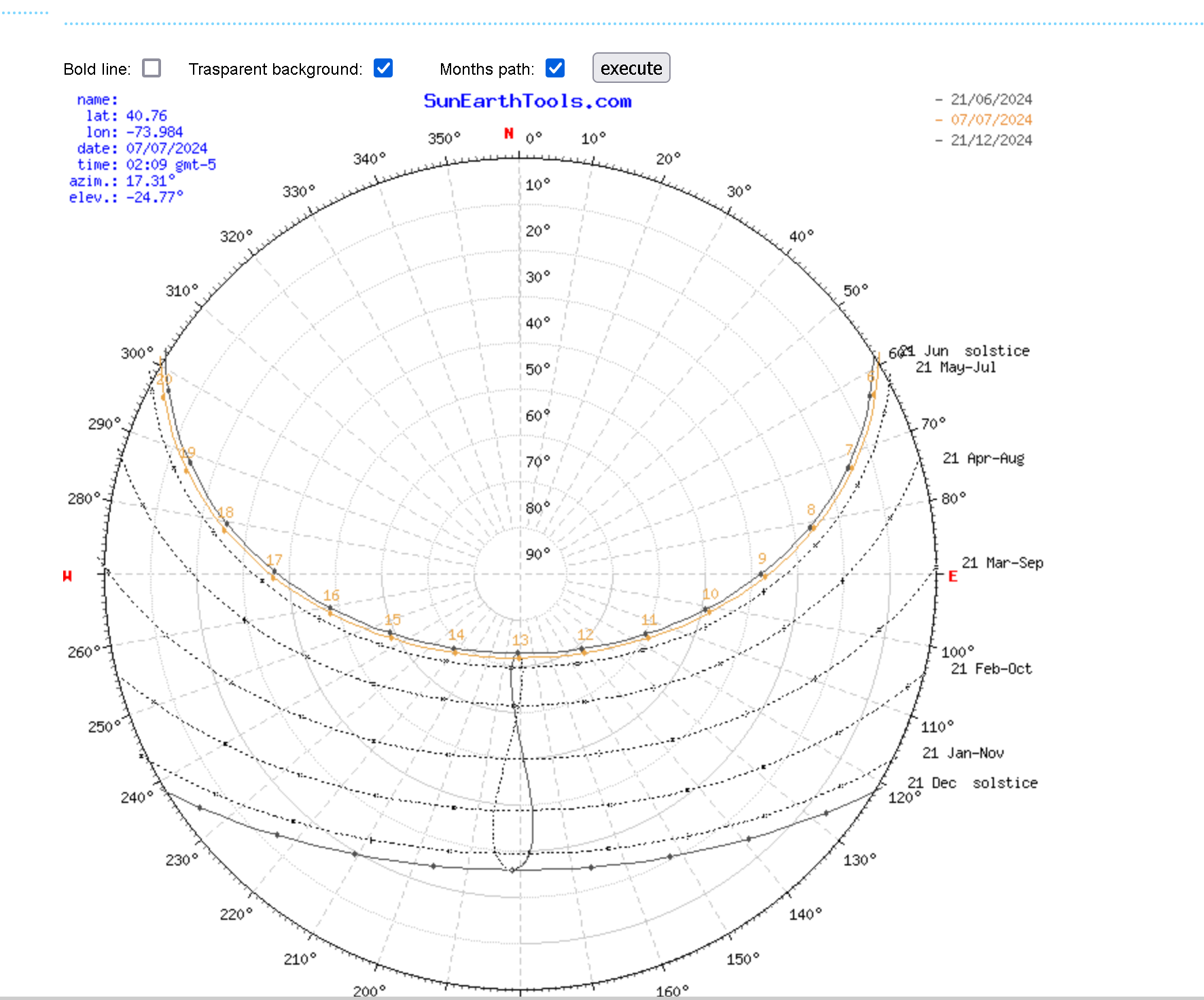
3d Sun path
[https://andrewmarsh.com/apps/staging/sunpath3d.html](https://andrewmarsh.com/apps/staging/sunpath3d.html)




#### Distance to the sun
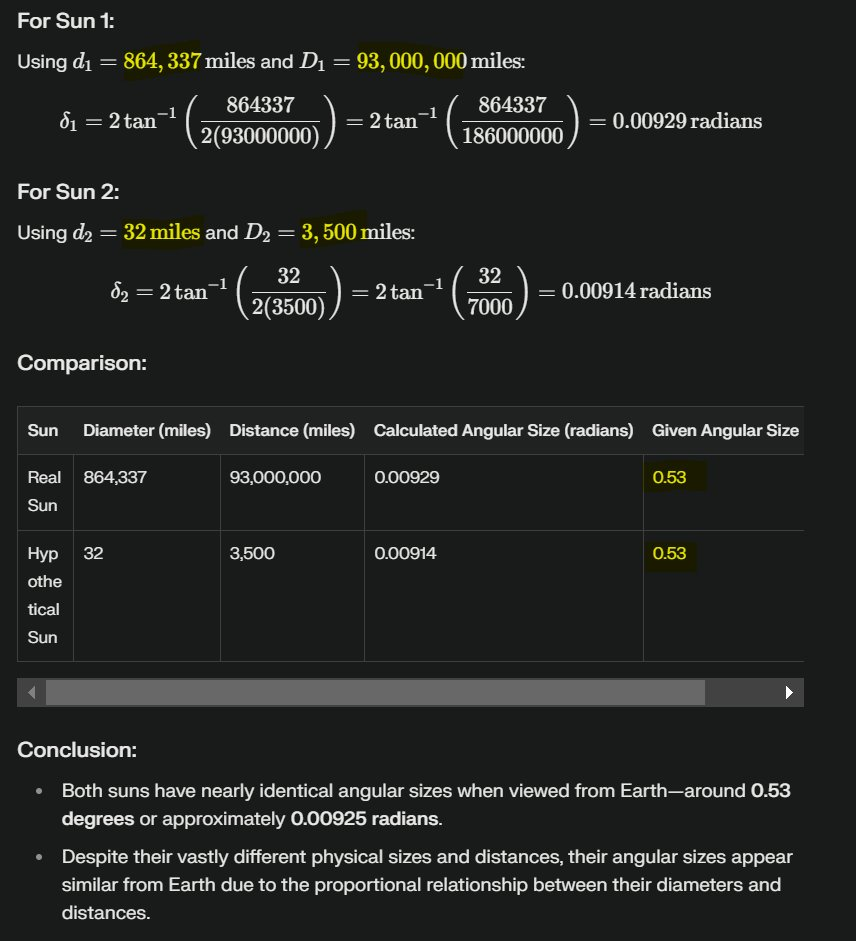
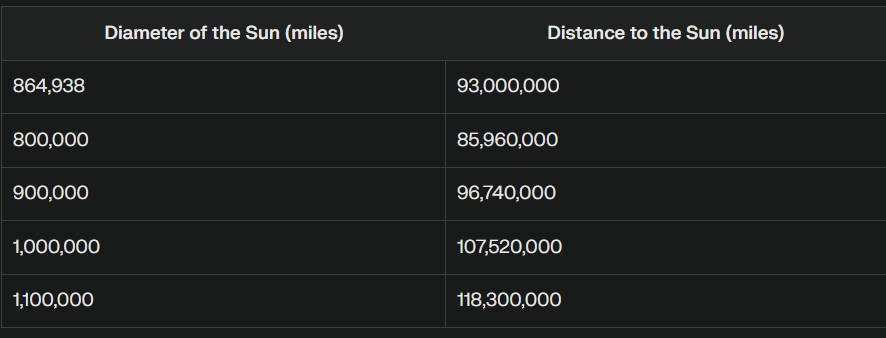
Alright, let's make sense of the provided formulas and concepts, and use them to find the distance to the Sun based on an angular size of 0.53 degrees.
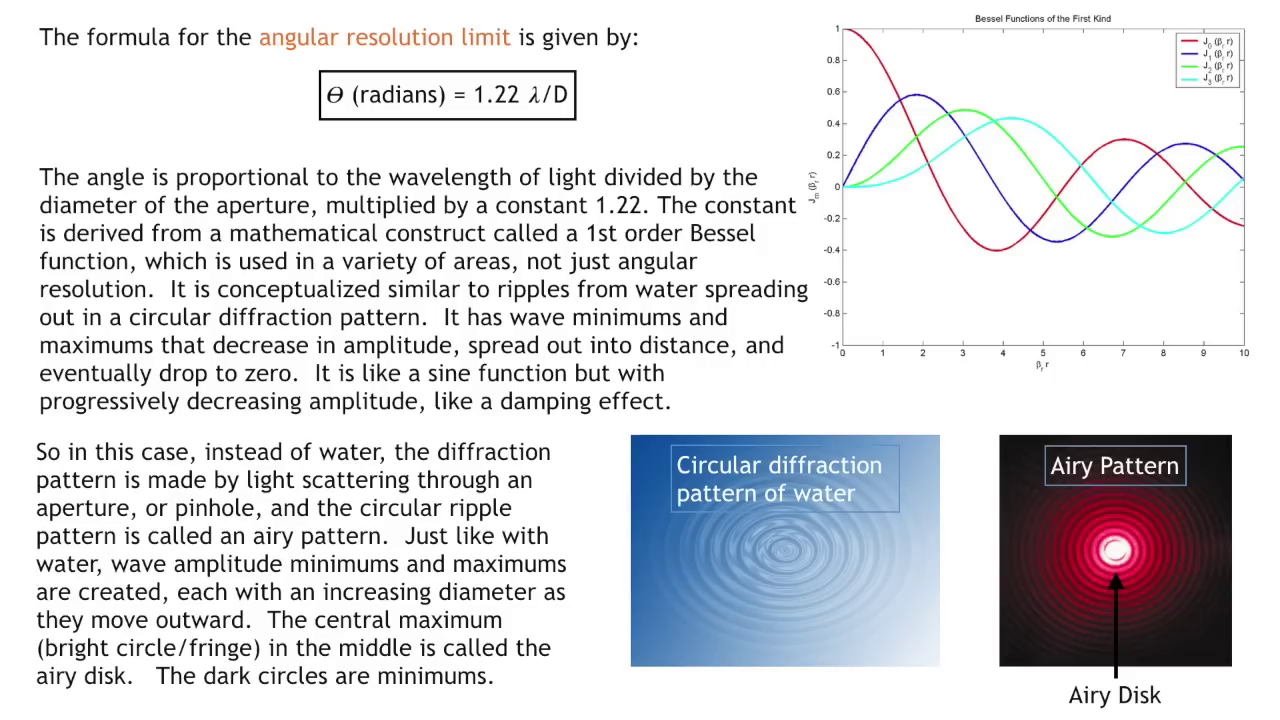
## **Angular Size Formula**
The angular size formula is given as:
δ=2tan^−1(d2D)
where:
- δ is the angular size (in radians or degrees).
- d is the actual diameter (or size) of the object.
- D is the distance from the observer to the object.










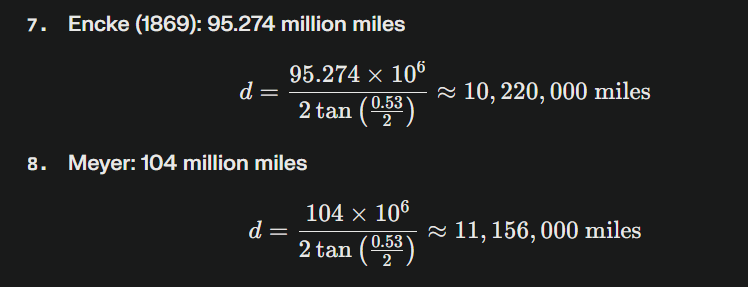
## **Step-by-Step Calculation**
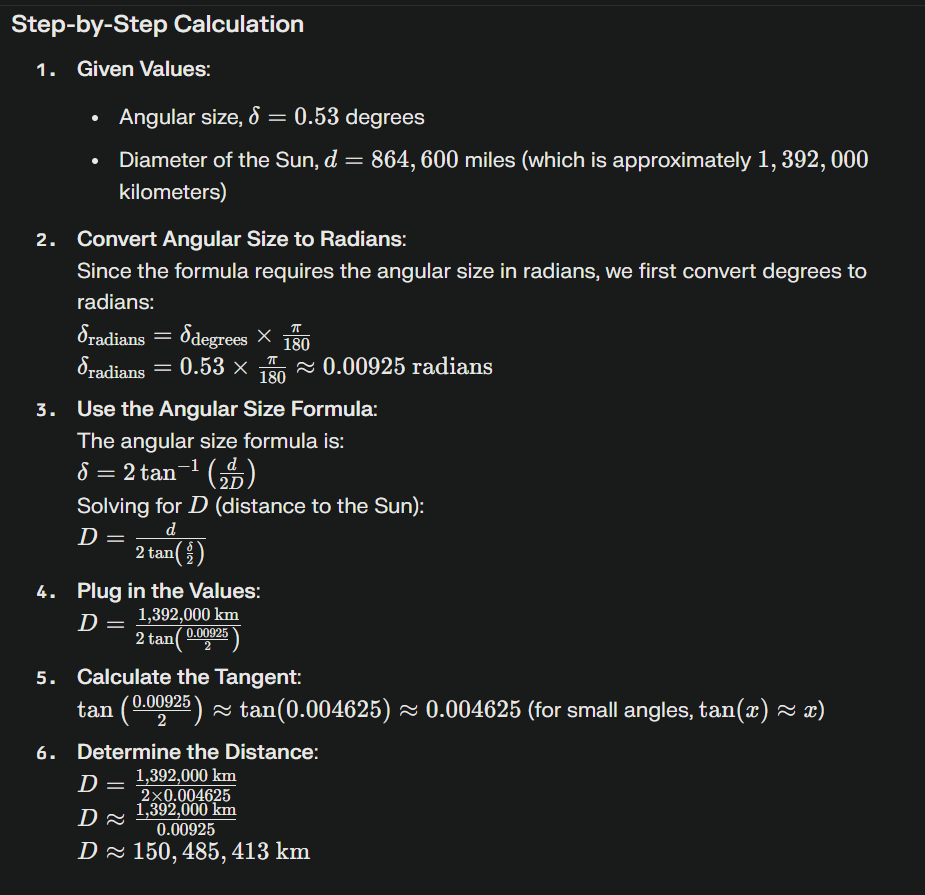
1. **Given Values**:
- Angular size, δ=0.53δ=0.53 degrees
- Diameter of the Sun, d=864,600d=864,600 miles (which is approximately 1,392,0001,392,000 kilometers)
2. **Convert Angular Size to Radians**:
Since the formula requires the angular size in radians, we first convert degrees to radians:
δradians=δdegrees×π180δradians=δdegrees×180π
δradians=0.53×π180≈0.00925 radiansδradians=0.53×180π≈0.00925 radians
3. **Use the Angular Size Formula**:
The angular size formula is:
δ=2tan−1(d2D)δ=2tan−1(2Dd)
Solving for DD (distance to the Sun):
D=d2tan(δ2)D=2tan(2δ)d
4. **Plug in the Values**:
D=1,392,000 km2tan(0.009252)D=2tan(20.00925)1,392,000 km
5. **Calculate the Tangent**:
tan(0.009252)≈tan(0.004625)≈0.004625tan(20.00925)≈tan(0.004625)≈0.004625 (for small angles, tan(x)≈xtan(x)≈x)
6. **Determine the Distance**:
D=1,392,000 km2×0.004625D=2×0.0046251,392,000 km
D≈1,392,000 km0.00925D≈0.009251,392,000 km
D≈150,485,413 kmD≈150,485,413 km



### Estimating the Distance to the Sun Using the Transit of Venus Method
To estimate the distance to the Sun without using the optical diameter of the Sun, we can use the transit of Venus method, which relies on parallax and trigonometry. Here are the steps and the key concepts involved:
### Key Concepts:
1. **Parallax**: The apparent shift in position of an object when viewed from two different locations.
2. **Transit of Venus**: When Venus passes directly between the Earth and the Sun, appearing as a small black dot moving across the Sun's disk.
3. **Timing the Transit**: By timing the duration of the transit from different locations on Earth, we can calculate the parallax angle.
### Steps to Calculate the Distance to the Sun:
1. **Observation Setup**:
- Place two observers at widely separated locations on Earth, ideally along the same meridian (longitude) but at different latitudes.
- Each observer records the exact times when Venus enters and exits the Sun's disk (first, second, third, and fourth contacts).
2. **Measure the Duration of the Transit**:
- Calculate the duration of the transit for each observer.
- The difference in the duration of the transit between the two locations is due to the parallax effect.
3. **Calculate the Parallax Displacement**:
- The parallax displacement (Δβ) is the angular separation between the two paths of Venus as seen from the two locations.
4. **Use Trigonometry to Calculate the Distance**:
- Letrebe the Earth-Sun distance andrvbe the Venus-Sun distance.
- The parallax displacementΔβcan be related to the distances using the formula:
Δβ=βs(rerv−1)
- Here,βsis the solar parallax angle, which can be calculated from the parallax displacement.
5. **Kepler's Third Law**:
- Use Kepler's Third Law to relate the distances of Earth and Venus from the Sun:
(rerv)3=(TeTv)2
- WhereTeandTvare the orbital periods of Earth and Venus, respectively.
### Example Calculation:
1. **Given Values**:
- Orbital period of Earth (Te): 365.25 days
- Orbital period of Venus (Tv): 224.7 days
- Parallax displacement (Δβ): Measured from observations
2. **Calculate the Ratio of Distances**:
rerv=(365.25224.7)2/3≈1.38248
3. **Calculate the Solar Parallax Angle**:
- AssumeΔβis measured to be a certain value (e.g., 0.01 degrees).
- ConvertΔβto radians:
Δβ=0.01×π180≈1.745×10−4radians
4. **Calculate the Earth-Sun Distance**:
- Rearrange the parallax formula to solve forre:
re=rv1−Δββs
- Sinceβsis the angle at which the Earth's radius is seen from the Sun, it can be approximated as:
βs≈Rere
- WhereReis the Earth's radius (approximately 6378 km).
Using the parallax displacement and the ratio of distances:
re≈rv1−1.745×10−46378re
- Givenrv≈0.72re(from Kepler's Third Law):
re≈0.72re1−1.745×10−46378re
- Solving forregives the Earth-Sun distance.
### Conclusion:
By using the transit of Venus and parallax measurements, we can estimate the distance to the Sun (the Astronomical Unit) without relying on the optical diameter of the Sun. This method involves precise timing of the transit from different locations on Earth and applying trigonometry and Kepler's laws to calculate the distance.
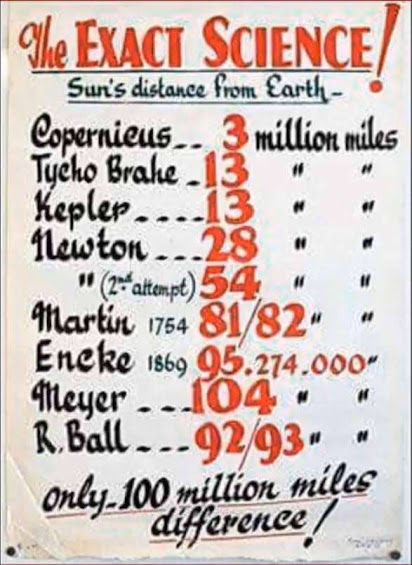
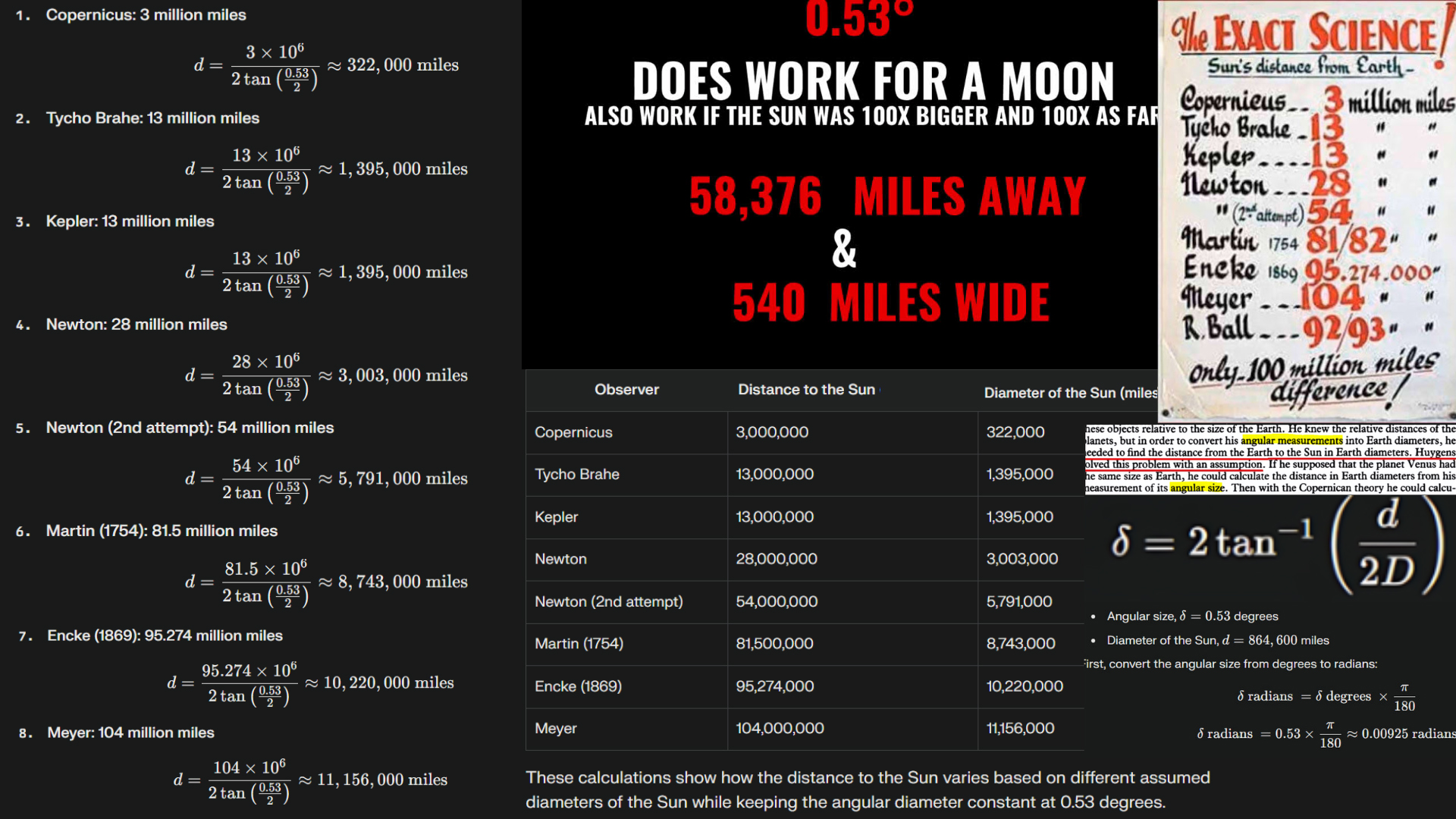
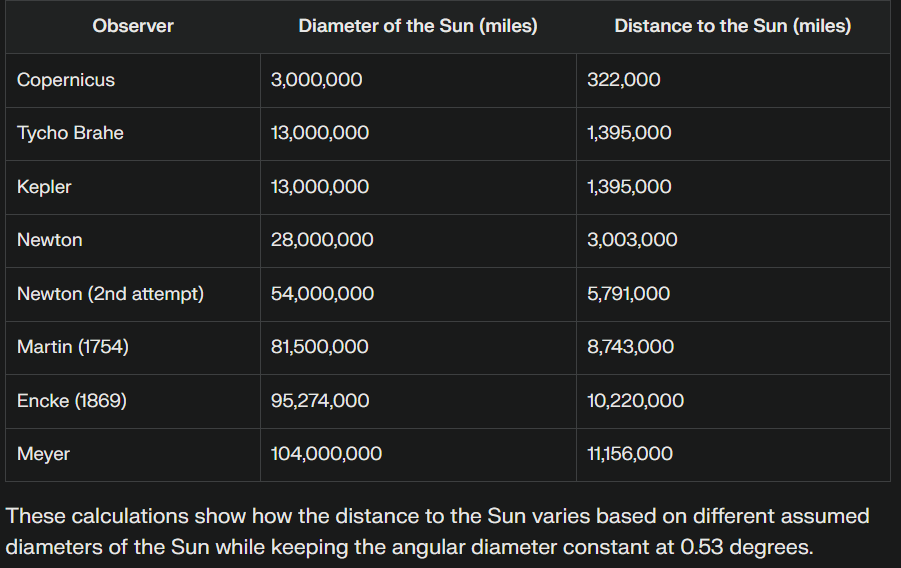
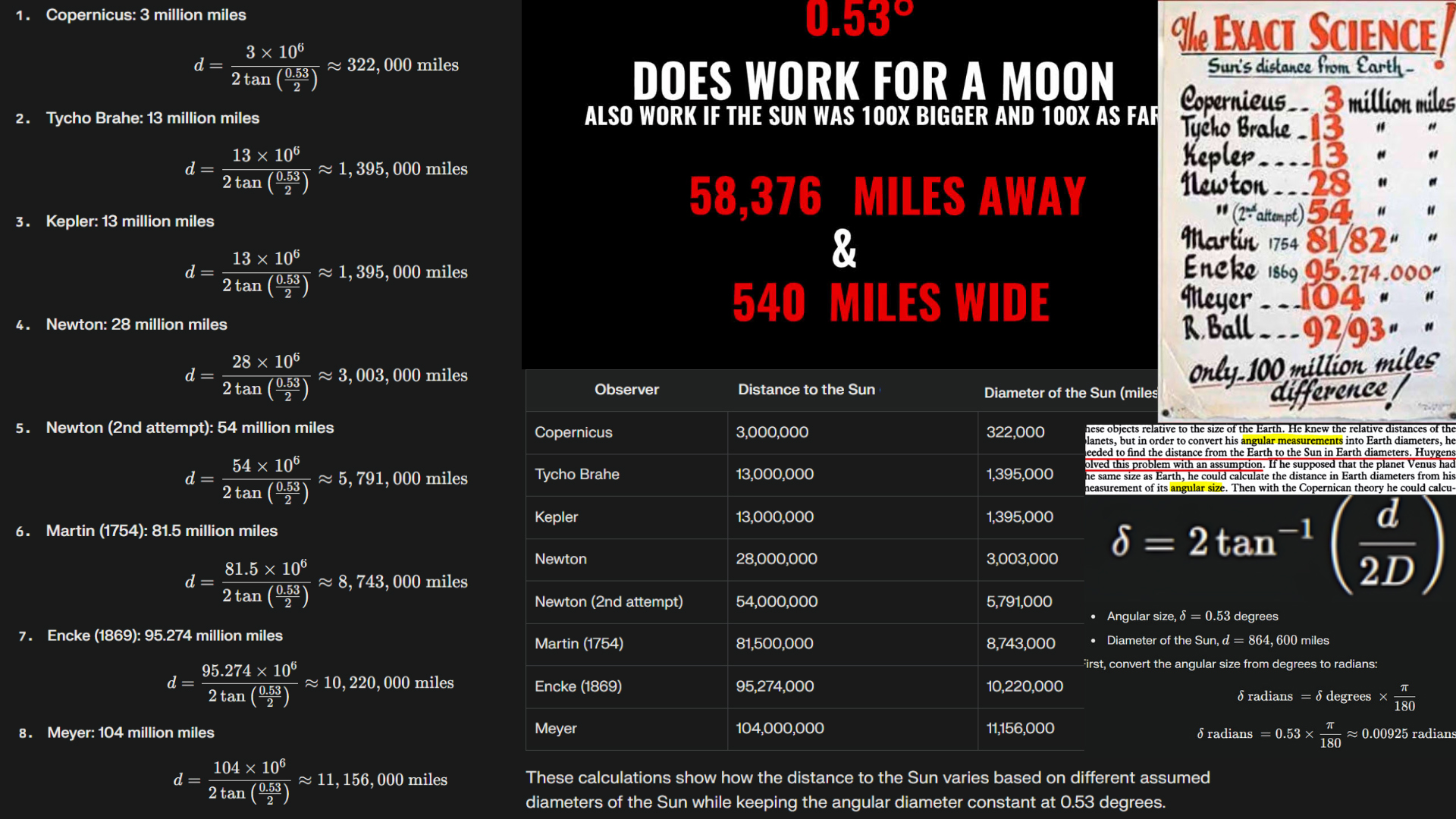
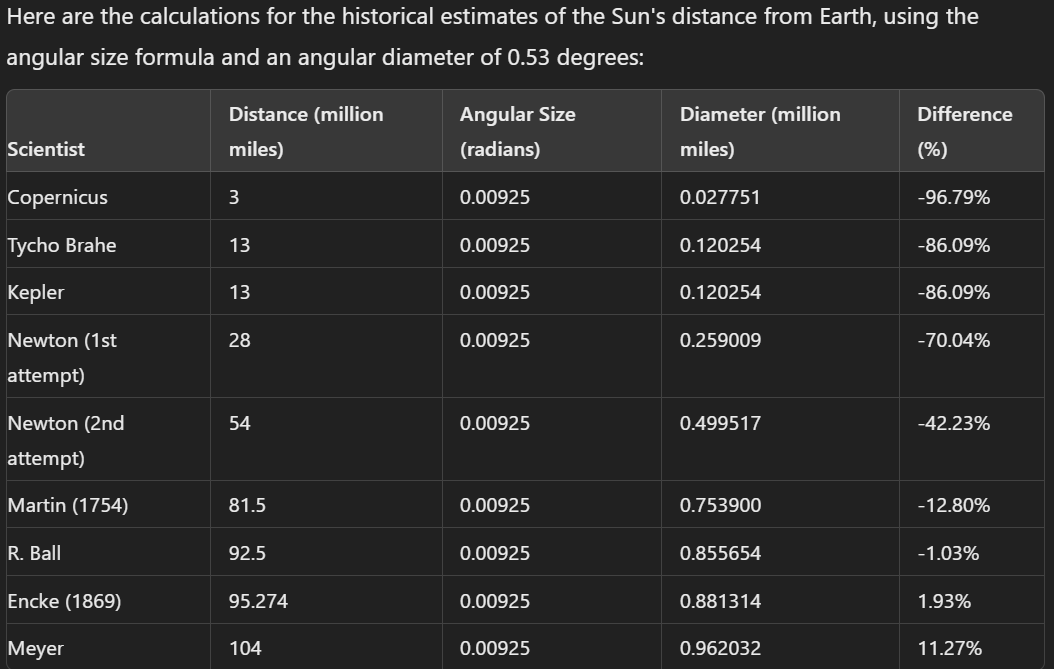
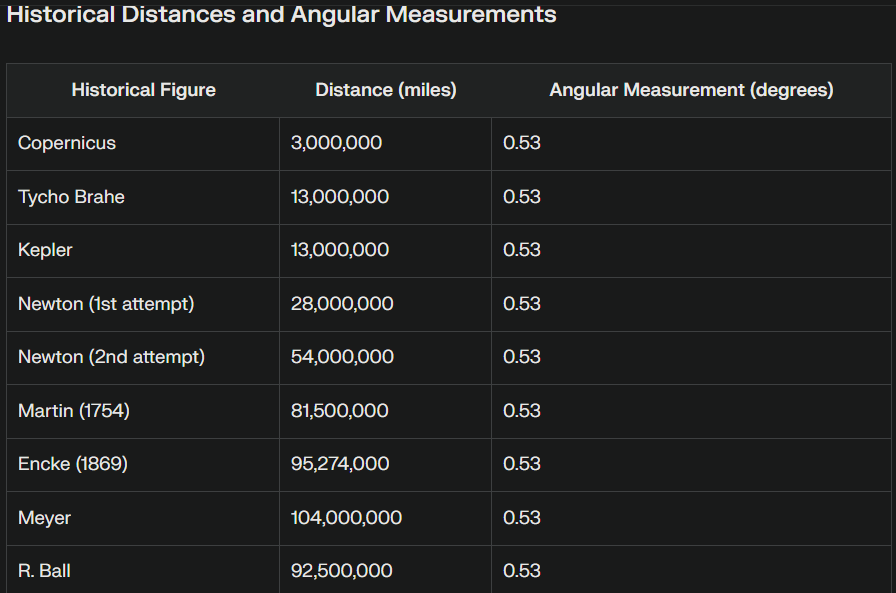
To estimate the distance to the Sun using different historical guesses, we can use the angular size formula provided. Here are the steps and calculations for each historical guess:
### Angular Size Formula:
The formula for angular size is:
δ=2tan−1(d2D)
### Given Values:
- Angular size,δ=0.53degrees (converted to radians:≈0.00925radians).
- Diameter of the Sun,d=864,600miles.
### Historical Guesses:
1. **Copernicus**: 3 million miles
2. **Tycho Brahe**: 13 million miles
3. **Kepler**: 13 million miles
4. **Newton**: 28 million miles
5. **Newton (2nd attempt)**: 54 million miles
6. **Martin (1754)**: 81/82 million miles (average: 81.5 million miles)
7. **Encke (1869)**: 95.274 million miles
8. **Meyer**: 104 million miles
9. **R. Ball**: 92/93 million miles (average: 92.5 million miles)
### Steps to Calculate the Angular Size for Each Distance:
1. **Convert the angular size from degrees to radians**:
δradians=δdegrees×π180δradians=0.53×π180≈0.00925radians
2. **Rearrange the formula to solve forD**:
D=d2tan(δ2)
3. **Calculate the distance for each historical guess**.
### Results:
Keeping the same Diameter of the sun...
1. **Copernicus**:
δ=2tan−1(8646002×3×106)≈16.4497degrees
2. **Tycho Brahe**:
δ=2tan−1(8646002×13×106)≈3.7966degrees
3. **Kepler**:
δ=2tan−1(8646002×13×106)≈3.7966degrees
4. **Newton**:
δ=2tan−1(8646002×28×106)≈1.7688degrees
5. **Newton (2nd attempt)**:
δ=2tan−1(8646002×54×106)≈0.9173degrees
6. **Martin (1754)**:
δ=2tan−1(8646002×81.5×106)≈0.6075degrees
7. **Encke (1869)**:
δ=2tan−1(8646002×95.274×106)≈0.5195degrees
8. **Meyer**:
δ=2tan−1(8646002×104×106)≈0.4763degrees
9. **R. Ball**:
δ=2tan−1(8646002×92.5×106)≈0.5353degrees
### Conclusion:
The angular size of the Sun varies significantly based on the historical guesses of the distance to the Sun. These calculations show how different estimates of the Sun's distance would affect its observed angular size.
- **Copernicus**: His estimate was far from accurate, resulting in a calculated diameter nearly 97% smaller than the actual diameter.
- **Tycho Brahe and Kepler**: Both had similar estimates with substantial inaccuracies.
- **Newton's Attempts**: His first attempt was less accurate than the second, but both significantly underestimated the Sun's diameter.
- **Martin (1754)**: His estimate was closer, with only a 12.8% discrepancy.
- **R. Ball and Encke (1869)**: Both came very close to the actual diameter, with R. Ball having only a slight underestimation.
- **Meyer**: Overestimated the diameter by about 11%.

Where did the AU (Astronomical Unit) really come from?
Given Values:
Orbital period of Earth (Te): 365.25 days
Orbital period of Venus (Tv): 224.7 days
Parallax displacement (Δβ): Measured from observations
Calculate the Ratio of Distances:
(Tv/Te)^2 = (365.25/224.7)^2 ≈ 2.6423
Apply Kepler's Third Law: Kepler's Third Law states that the square of the orbital period ratio is proportional to the cube of the semi-major axis ratio:
(Tv/Te)^2=(ae/av)^3
where ae and ava are the semi-major axes (average distances from the Sun) of Earth and Venus, respectively.
Rearrange to solve for the semi-major axis ratio
(av/ae)^3=2.6423
If we know the average distance from Venus to the Sun (avav) in terms of AU (let's assume avav is approximately 0.72 AU, which is a known value from astronomical measurements), we can find the Earth-Sun distance:
av/ae=(3sqrt)2.6423≈1.375
By using the orbital periods of Earth and Venus and applying Kepler's Third Law, we can estimate the Earth-Sun distance (AU) without relying on the Sun's apparent diameter or angular size. This method leverages the relationship between orbital periods and distances.
If we know the average distance from Venus to the Sun (avav) in terms of AU (let's assume avav is approximately 0.72 AU, which is a known value from astronomical measurements), we can find the Earth-Sun distance:
a / e=1.375×0.72 AU≈0.99 AU
OR. How they claim to have done it:
Calculate the Solar Parallax Angle:
Assume Δβ is measured to be a certain value (e.g., 0.01 degrees).
Convert Δβ to radians:
Δβ=0.01×π180≈1.745×10−4 radians
Calculate the Earth-Sun Distance
Rearrange the parallax formula to solve for re:
re=rv1−Δββs
re=1−βsΔβrv
Since βs is the angle at which the Earth's radius is seen from the Sun, it can be approximated as:
βs≈Re
Where Re is the Earth's radius (approximately 6378 km).
Using the parallax displacement and the ratio of distances:
re≈rv1−1.745×10−46378 re≈1−re63781.745×10−4rv
Given rv≈0.72
rerv≈0.72re (from Kepler's Third Law):
re≈0.72 re1−1.745×10−46378rere≈1−re63781.745×10−40.72re
Solving for re gives the Earth-Sun distance. Yielding 1 AU.
So without the radius value, there is no AU.
That radius value belongs to us, as it is a function of optics. Since no one has ever substantiated physical earth curve as a mechanism of anything, the math basis for the optic limits causing the illusion of bottom up obstruction on a flat plain is the prevailing most substantiated position.
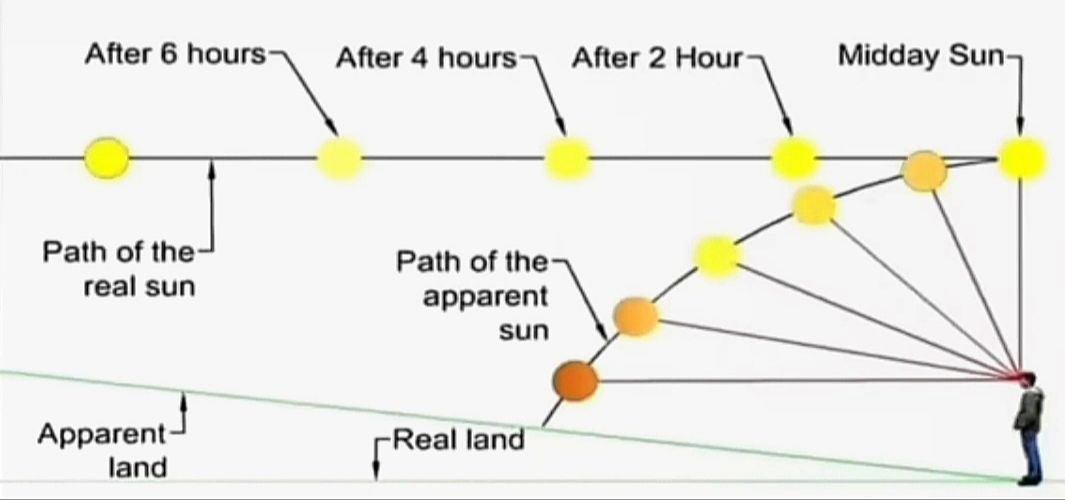
### Sunsets
Can we see infinitely?
The Sun
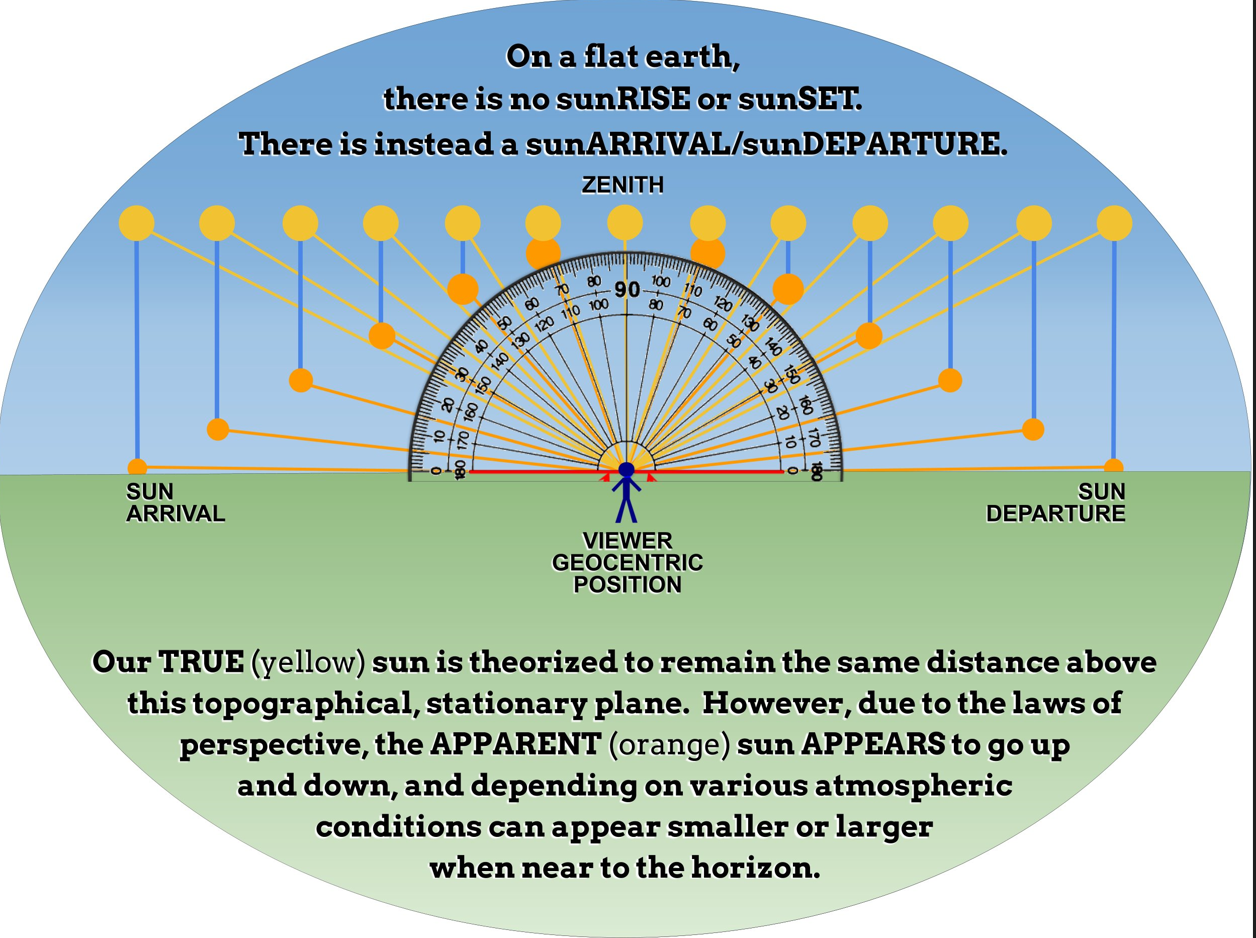
If the Earth was flat, How could the Sun set?
Equal on all map projections
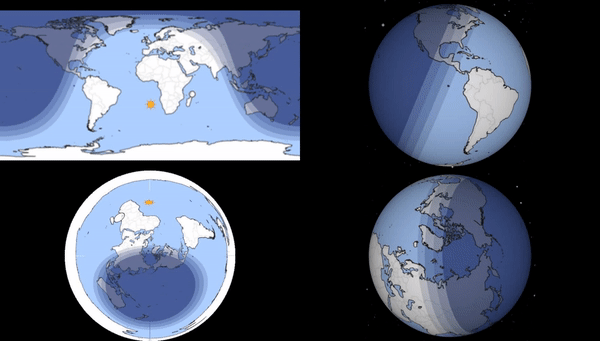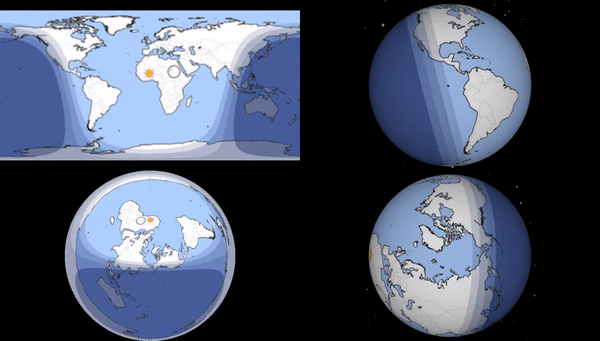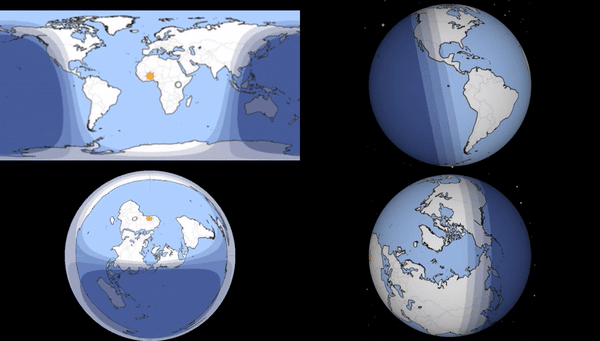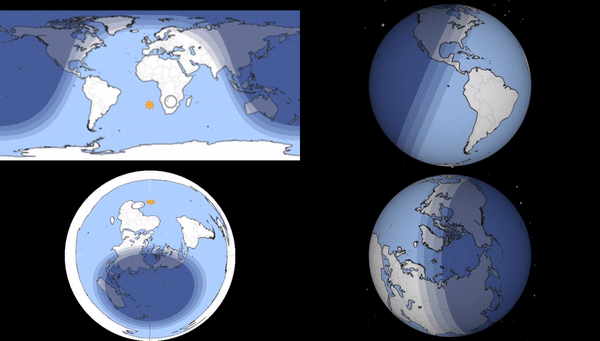
[https://www.reddit.com/r/MoonKnight/comments/u47xsd/the_figure_8_plot_analemma_in_ep3s_sky_reel/?utm_source=share&utm_medium=mweb3x&rdt=45688](https://www.reddit.com/r/MoonKnight/comments/u47xsd/the_figure_8_plot_analemma_in_ep3s_sky_reel/?utm_source=share&utm_medium=mweb3x&rdt=45688)
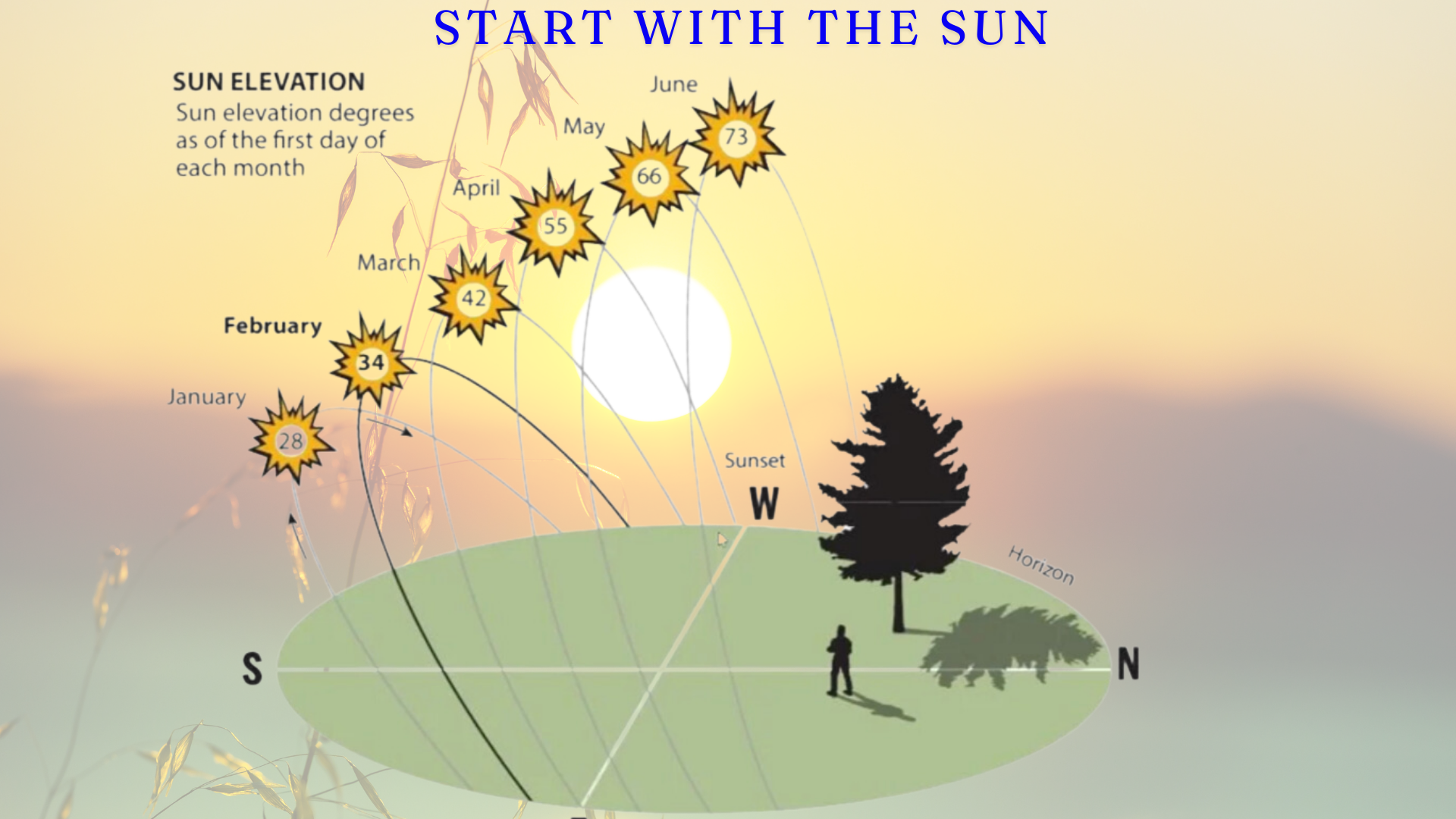
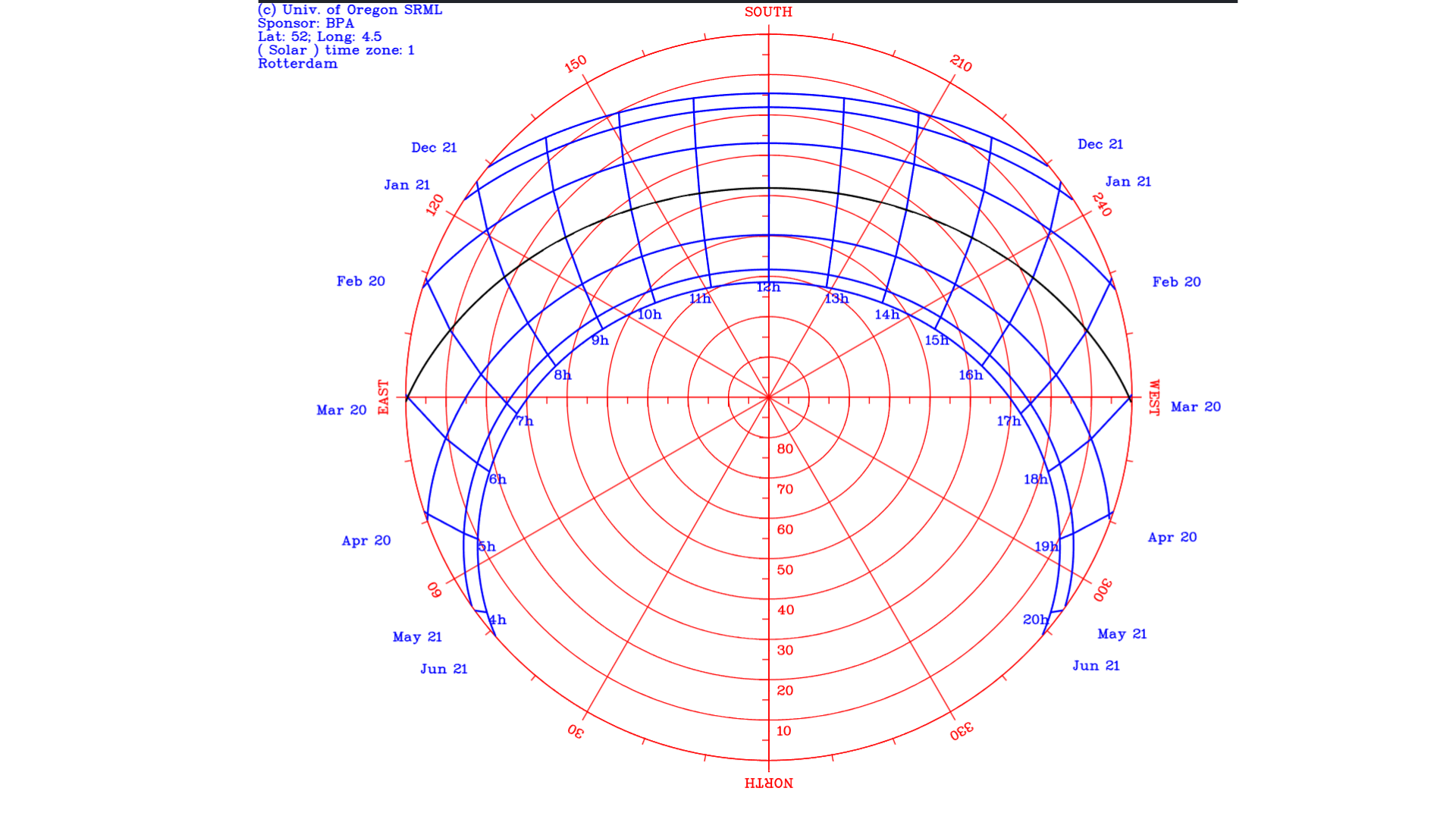
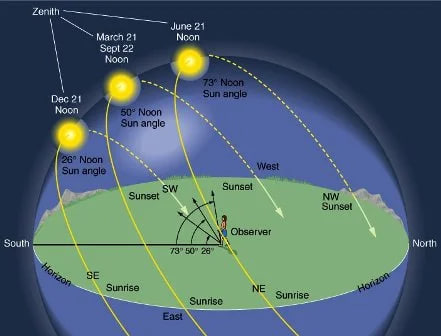
# Sun angles in Australia
# day/night, Seasons, Equinox, and 24 hour daylight on Flat Earth
.png)

.png)
## The Luminaries
.jpg)


## Tweets
Here are 11 posts where I address sunsets ...
In text.
With images.
With memes.
With infographics.
With substantive specificity.
In video. In audio.
Every which way I possibly could.
Please stop 😅
But, if the earth were flat, how would the sun ever set?
The sun never sets:
Sunsets prove flat earth: [https://x.com/AntiDisinfo86/status/1820648319493804191](https://x.com/AntiDisinfo86/status/1820648319493804191)
The sun never sets video:
Like this:
Sun Fade Out Compilation [Even with Solar Filter]
Sun Fade out
AngulaR size change?
Sunrise south of east and set south of west:
AETHER COSMOLOGY CREW AND THE SUN
THE SHADOWS OF THE SUN DEBUNK THE GLOBE
The sun and the celestial sphere:






Why does the sun appear to set?
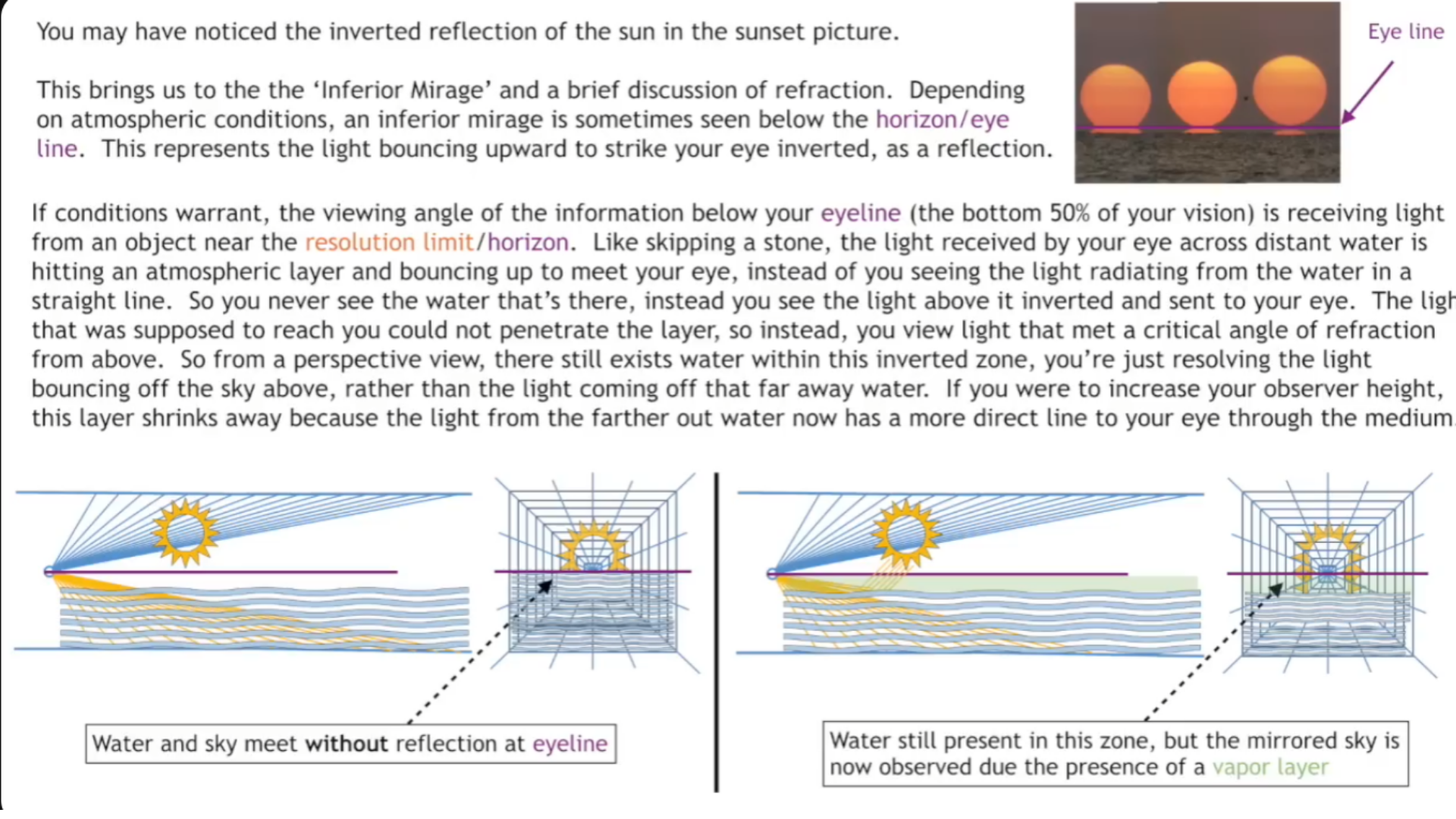
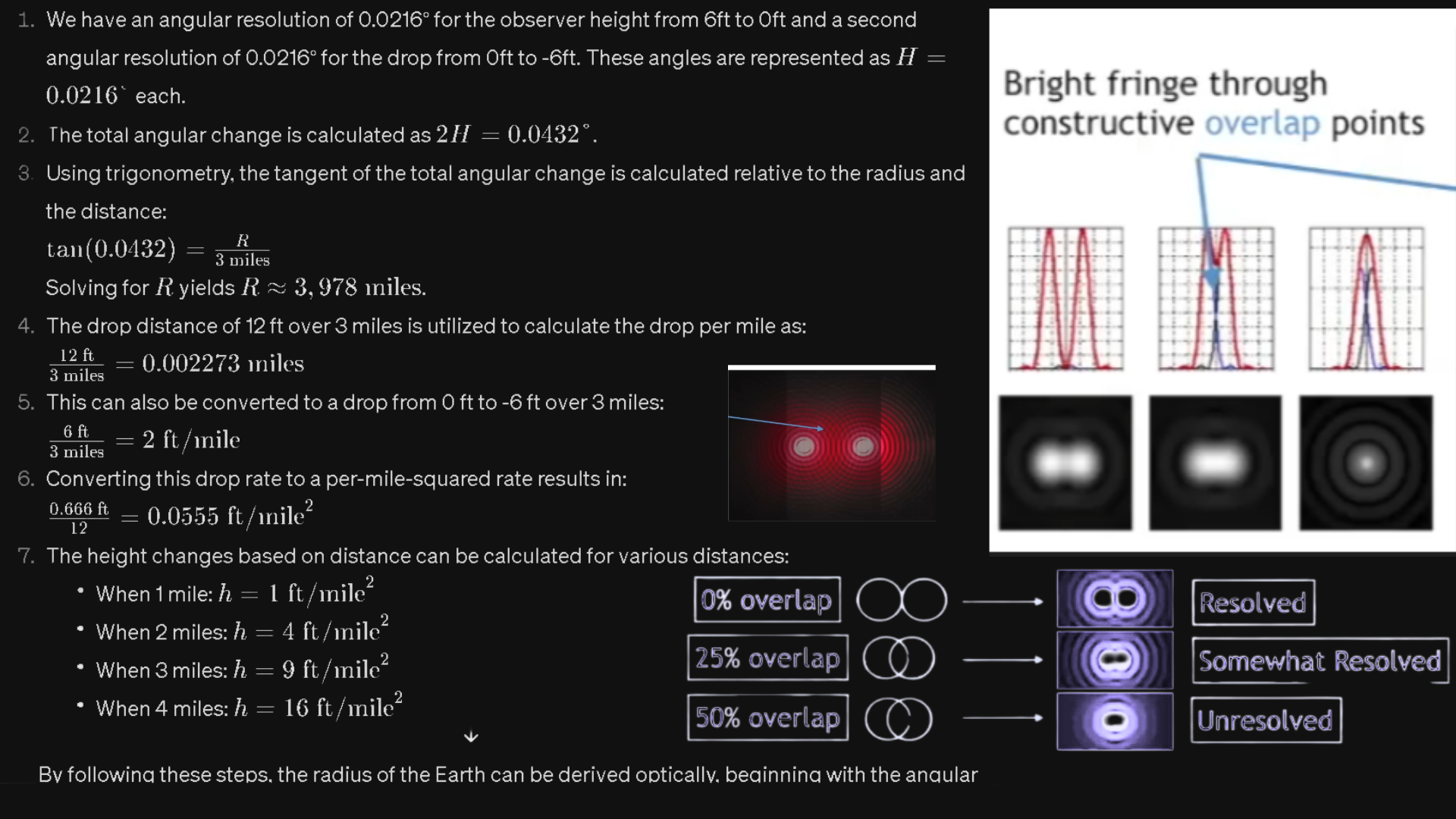
Inverse Square Law: Explains the diminishing intensity of light with distance, contributing to the fading and disappearance of distant objects. Perspective and Angular Resolution: Affect how objects are perceived and when they become unresolvable. Atmospheric Effects: Modify the light path, affecting the appearance and brightness of objects.
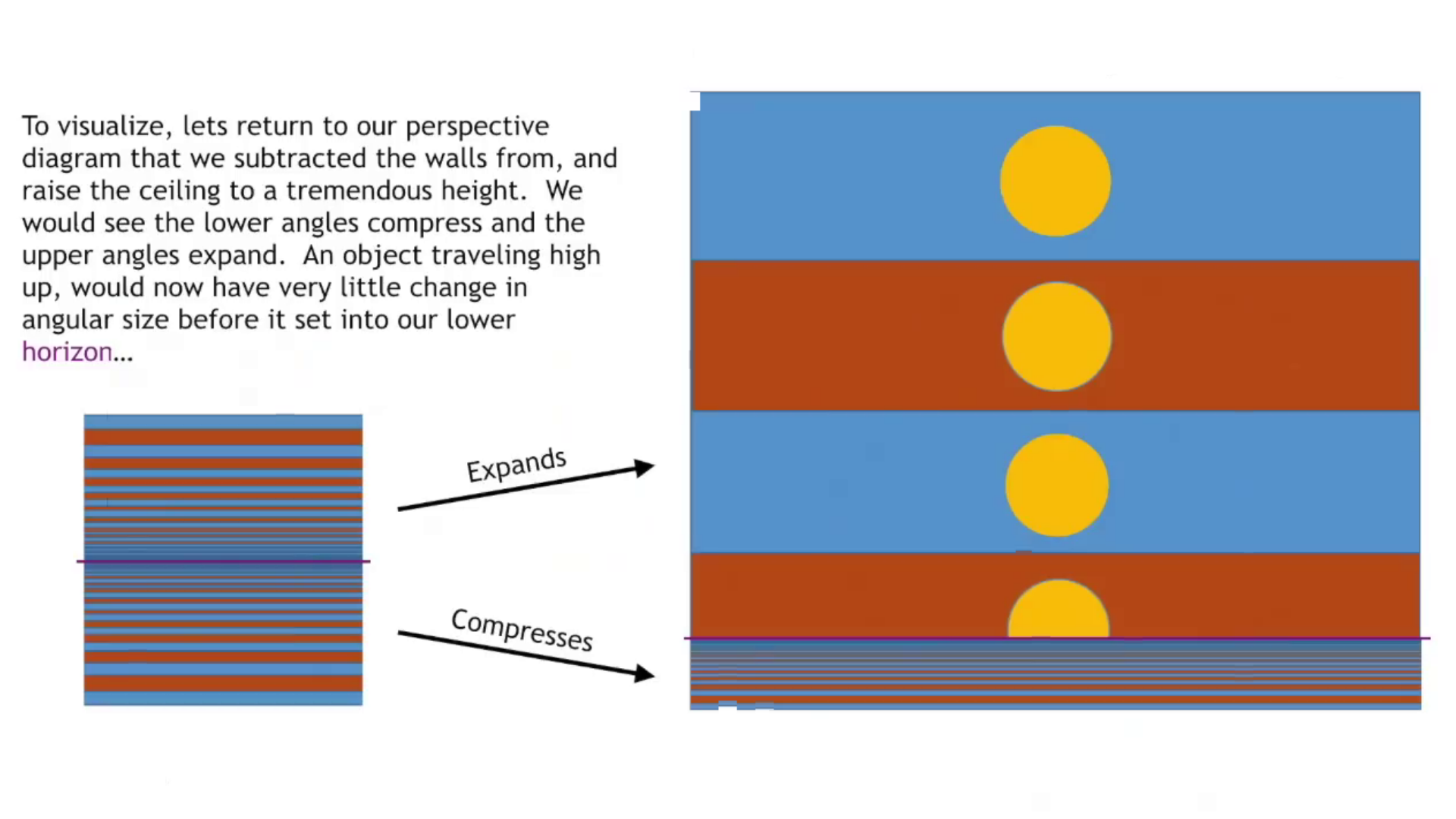
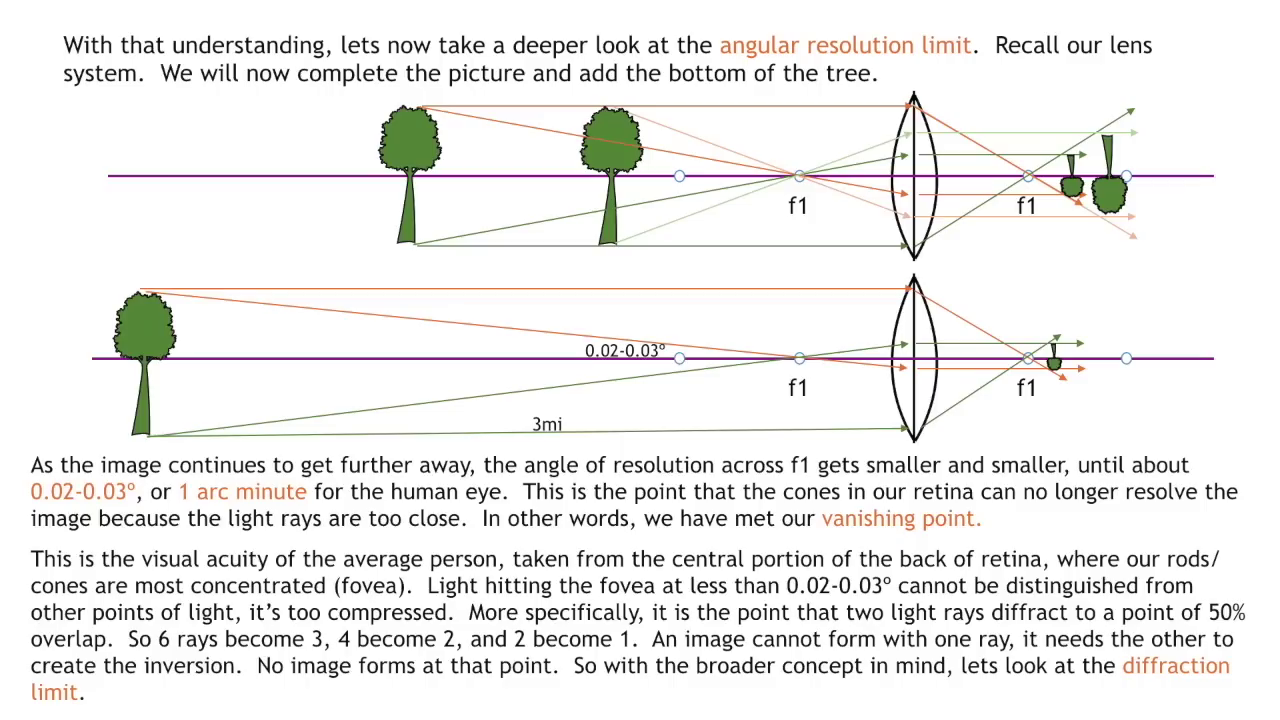
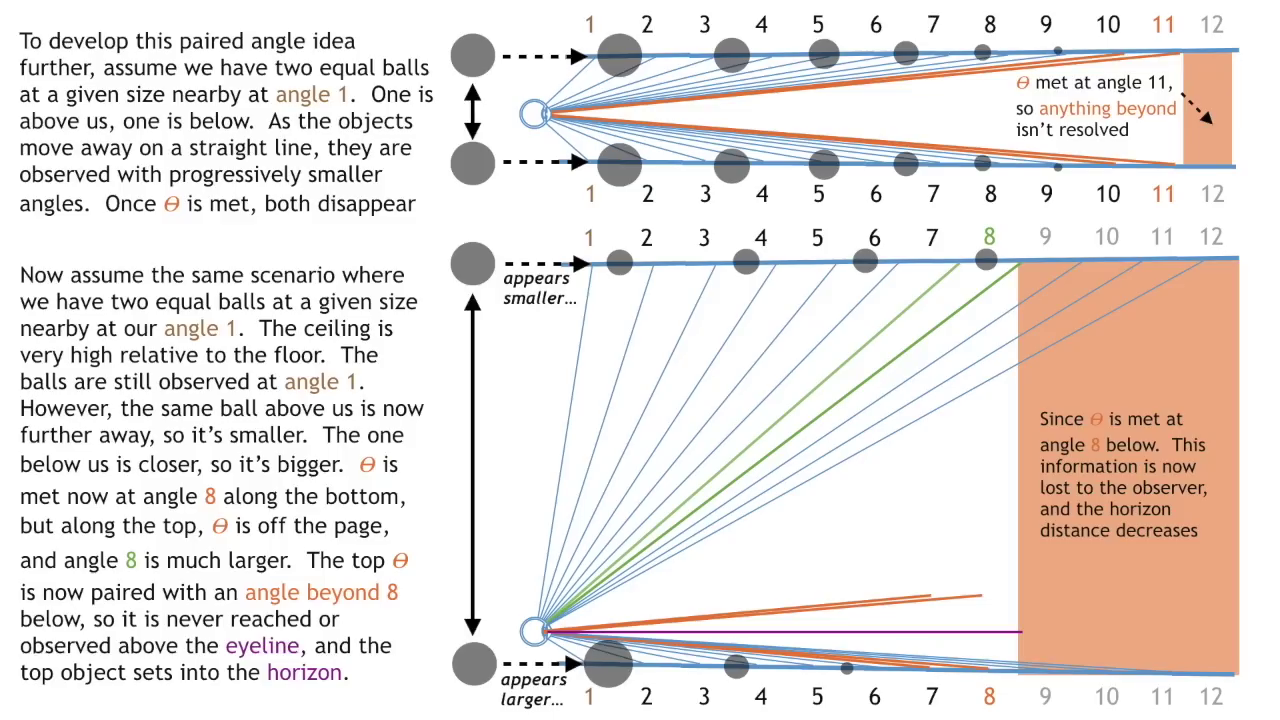
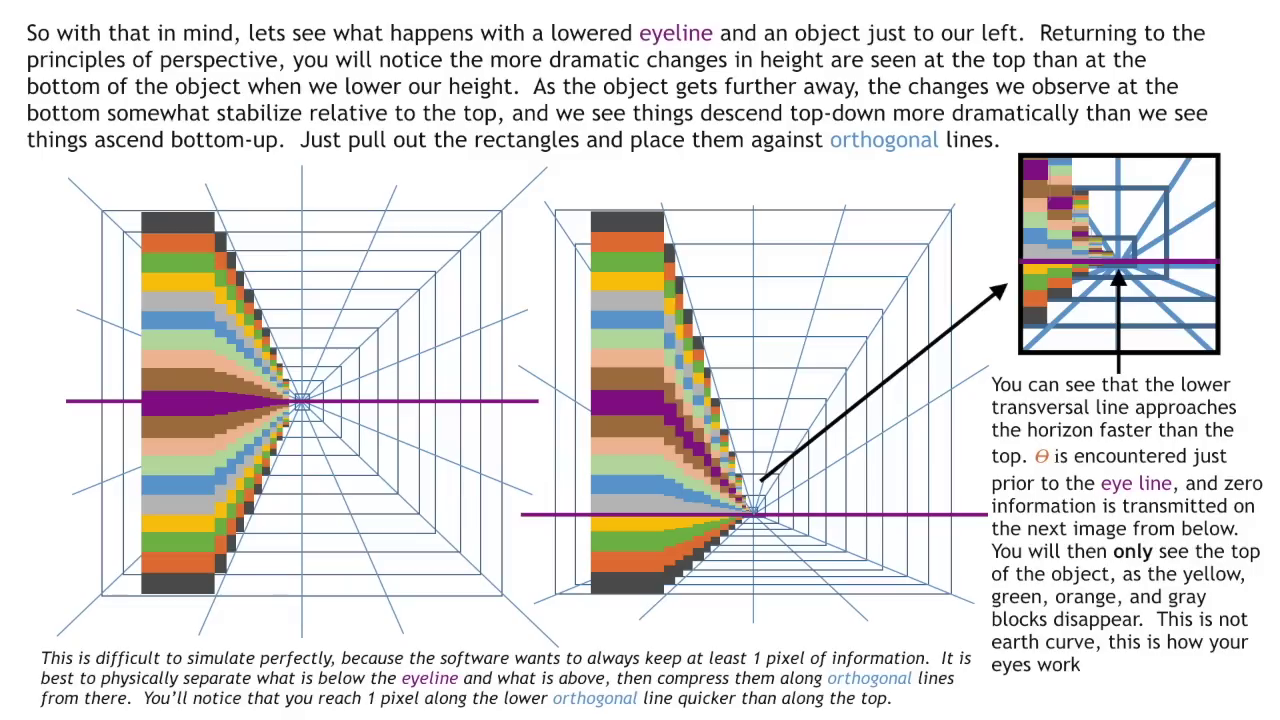
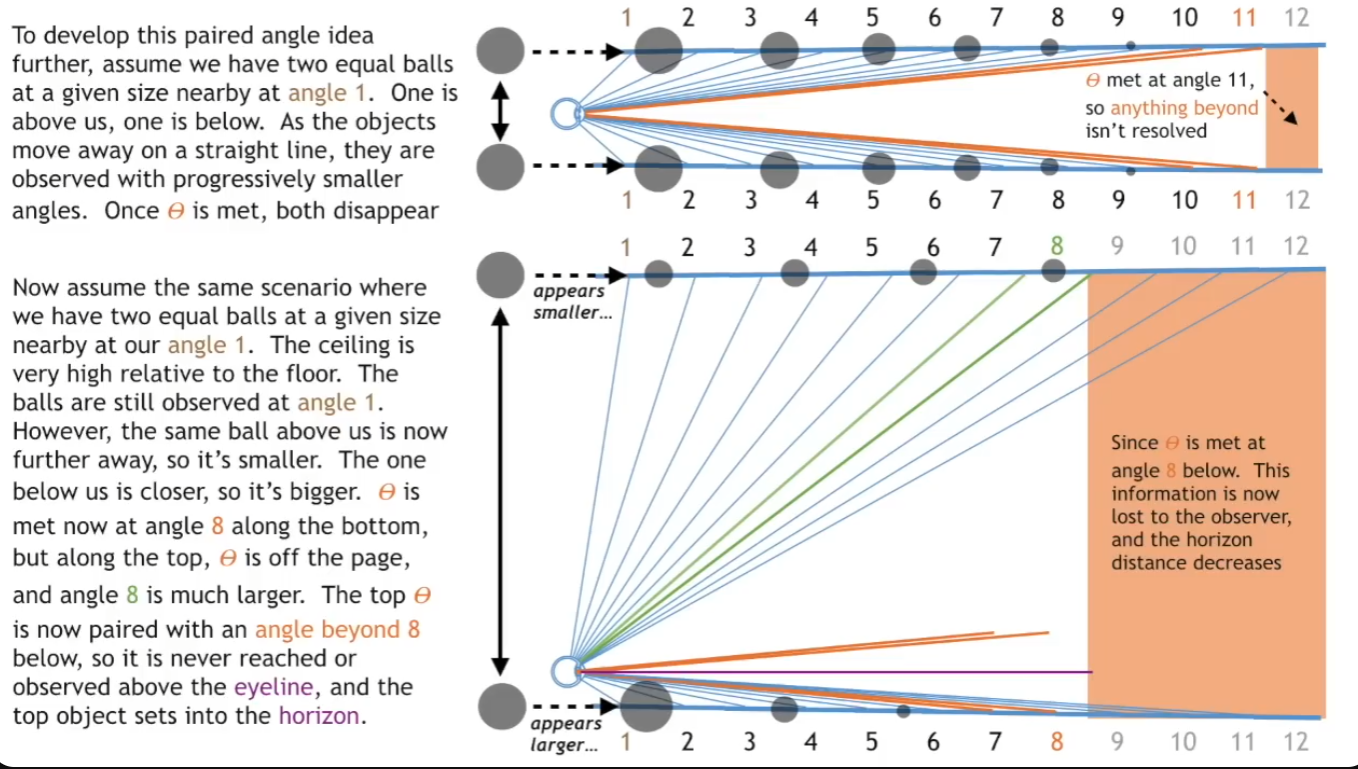
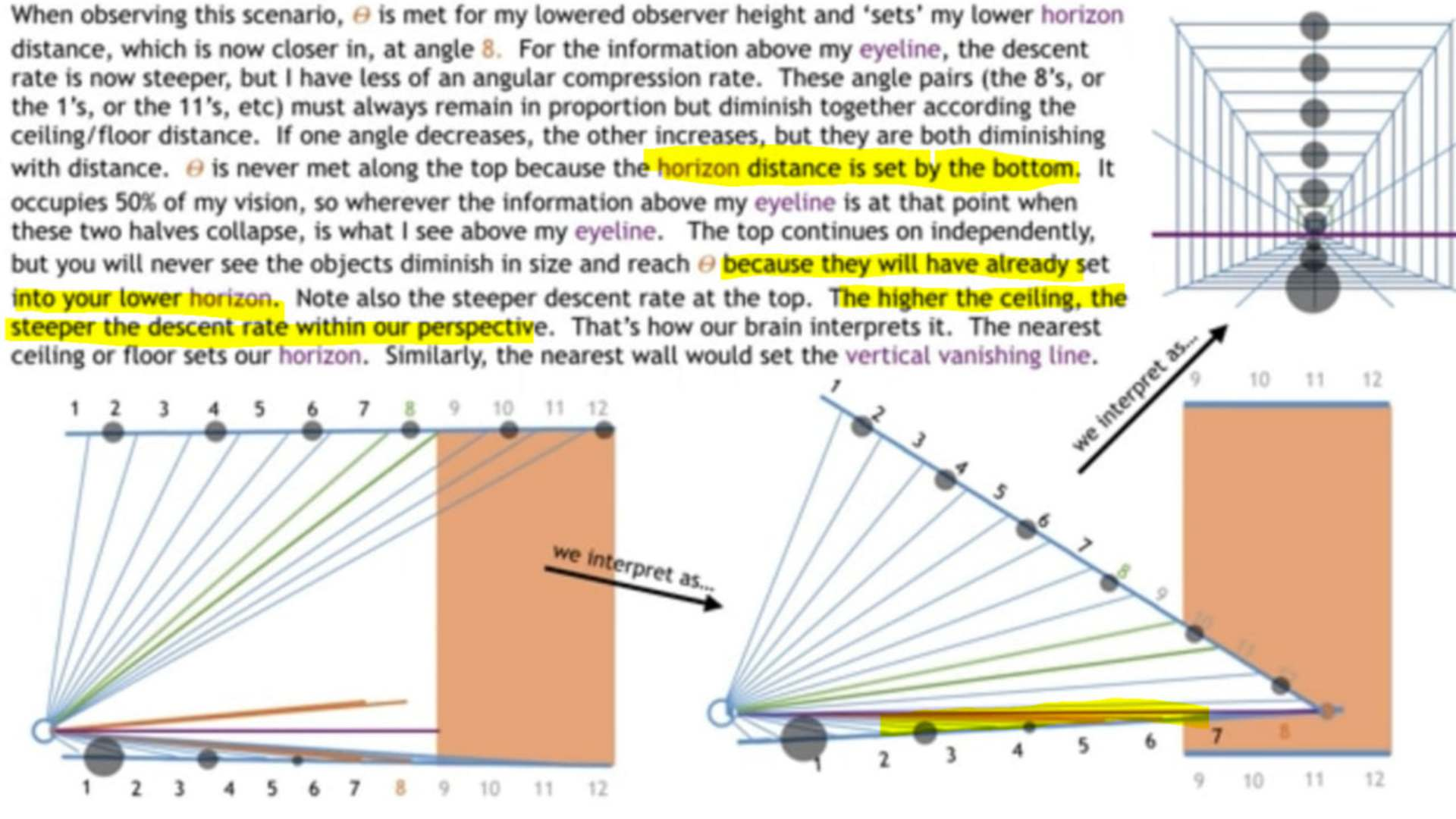
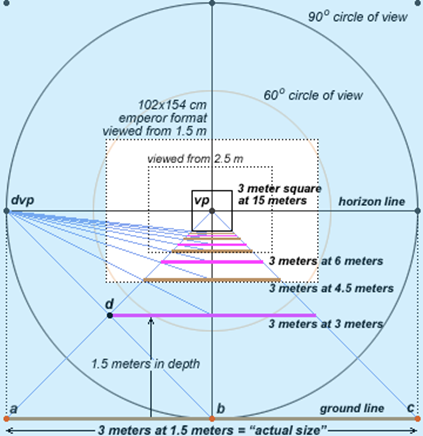
The Sun never sets.... it only moves far enough away to become unresolvable, and eventually takes its daylight with it. Perspective, observer height, the diffraction limit, the attenuation of light, and angular resolution limit all contribute to the visual phenomenon of objects appearing to disappear bottom-up at a distance. The eye's resolution angle, which is the minimum angle at which two points can be distinguished as separate, also plays a crucial role in the perception of objects at a distance. They also illustrate that there is a specific angle at which objects disappear from sight, referred to as Θ (theta), and this angle is reached sooner for objects below the eye line. Keep in mind that for the object to disappear entirely, or become completely unresolvable, theta must be diminished to zero both above and below. The images below illustrate how angles of sight compress or expand based on the observer's height and how objects of different heights are perceived by the human eye. They convey that as an observer lowers their height, the angles close to the ground compress, making the horizon appear closer. Changing the observer's height affects the angles of sight, compressing them more at the bottom (ground level) than at the top (sky level). This alteration results in a change in how information is visually processed and how far one can see. Conversely, the angles above expand. An object traveling at a higher altitude would show little change in angular size before it sets into the lower horizon. Although the total number of potential angles of vision above and below the eye line is the same, the compression rate of these angles differs. This variance in compression affects how objects are visually perceived as they move away from the observer. Objects can seem to disappear or "set" into the horizon or other larger objects (like buildings) when viewed from certain angles. When one looks up at a very steep angle, the floors towards the top of a building compress visually, making it harder to discern details or even see the highest floors. This compression of angles leads to a loss of information and contributes to the "disappearance" of objects that are not actually obscured by any physical barriers. Also, there are of course atmospheric conditions such as aberrations and refraction that can alter the perceived size and shape of distant objects. The higher the ceiling, the steeper the angular compression, and the faster the descent rate to the vanishing line. This is EXACTLY how the sun and moon appear to set, maintaining a relatively constant size due to their high upper boundary and short travel distance within the observer's perspective before they meet the horizon line.




# The Sun
%201%201%201%201%201%201%201%201%201%201%201%201.jpg)
## Ecliptic


## Light Distribution



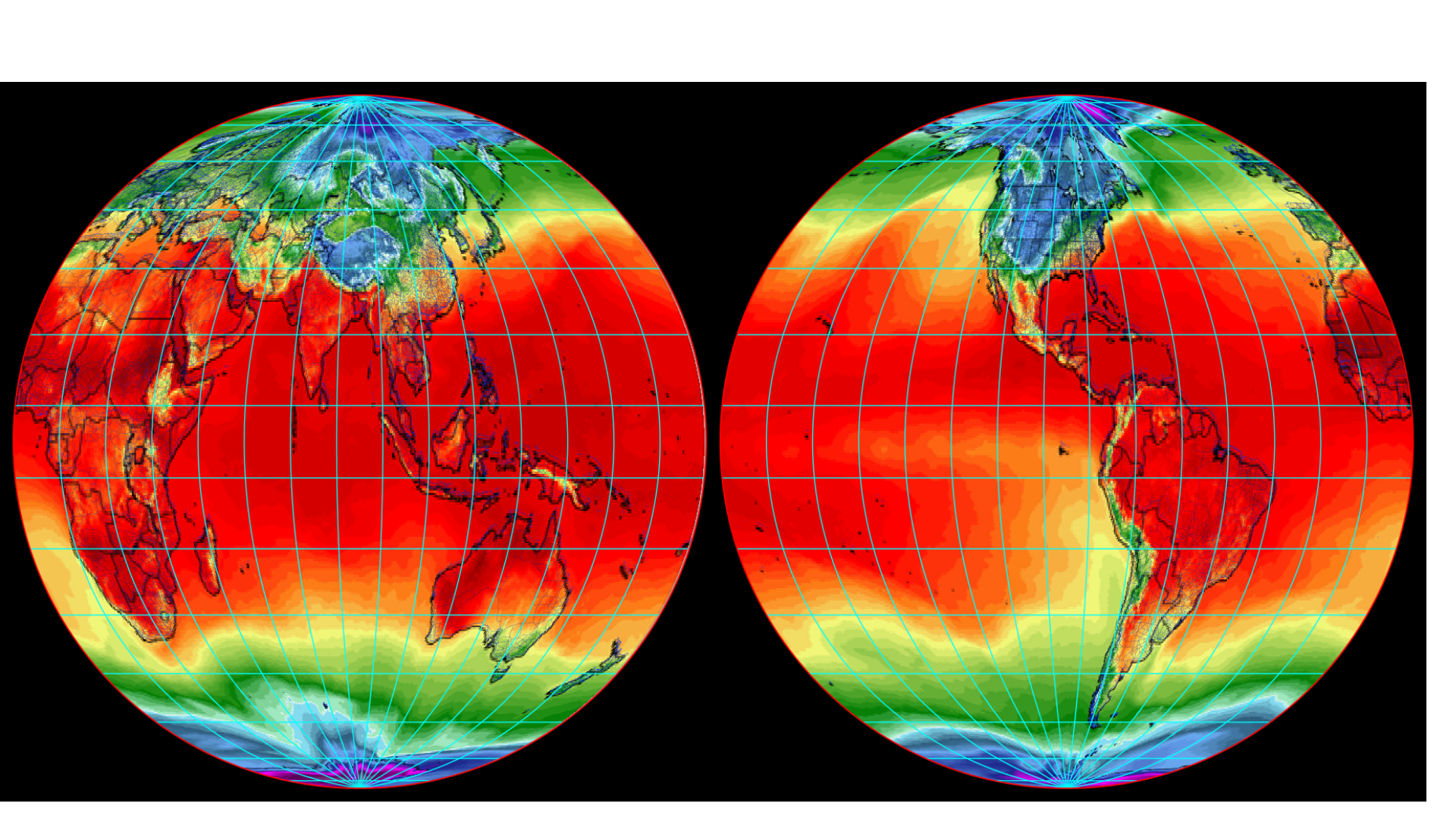
Completely equal....forced equality even.... since it is taking the light distribution across the earth and forcing it onto each projection.
.gif)
[https://x.com/AntiDisinfo86/status/1762701556778971200](https://x.com/AntiDisinfo86/status/1762701556778971200)
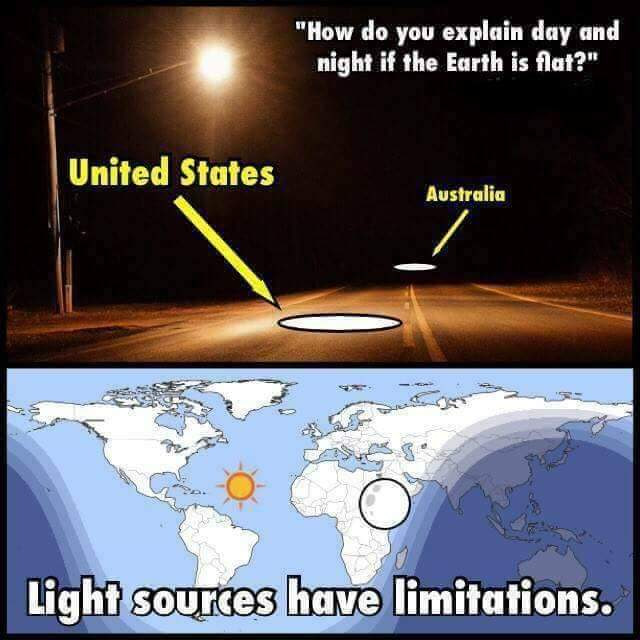
"You cant show day and night and seasons on same model...
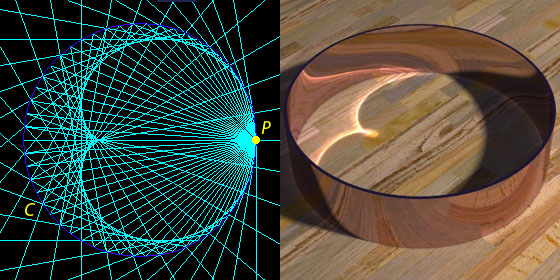
### Coffee Cup Caustic
[https://www.youtube.com/watch?v=SYAnW-LniPM&ab_channel=MathPhysicsEngineering](https://www.youtube.com/watch?v=SYAnW-LniPM&ab_channel=MathPhysicsEngineering)

.jpg)
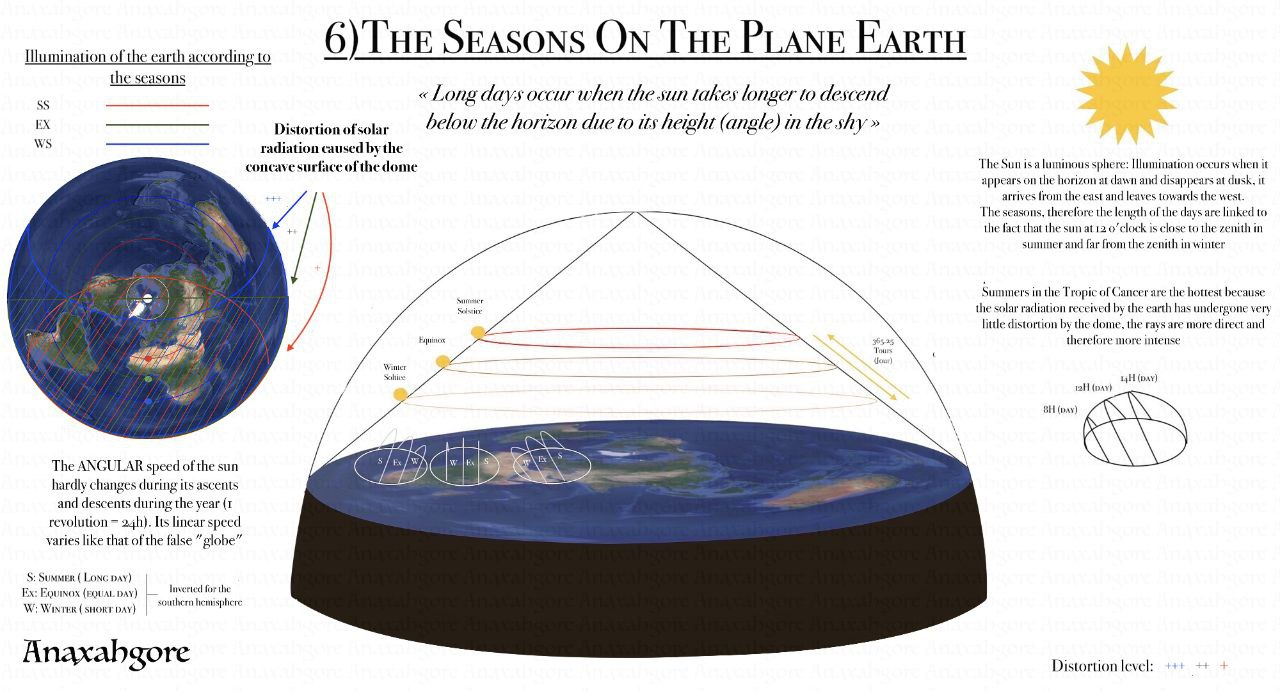
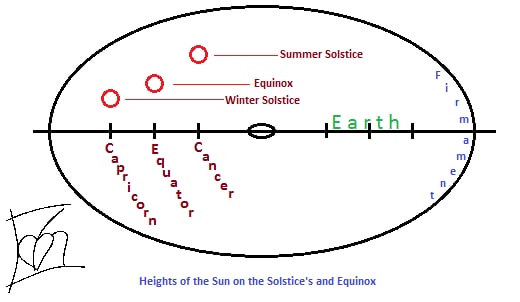
## Seasons
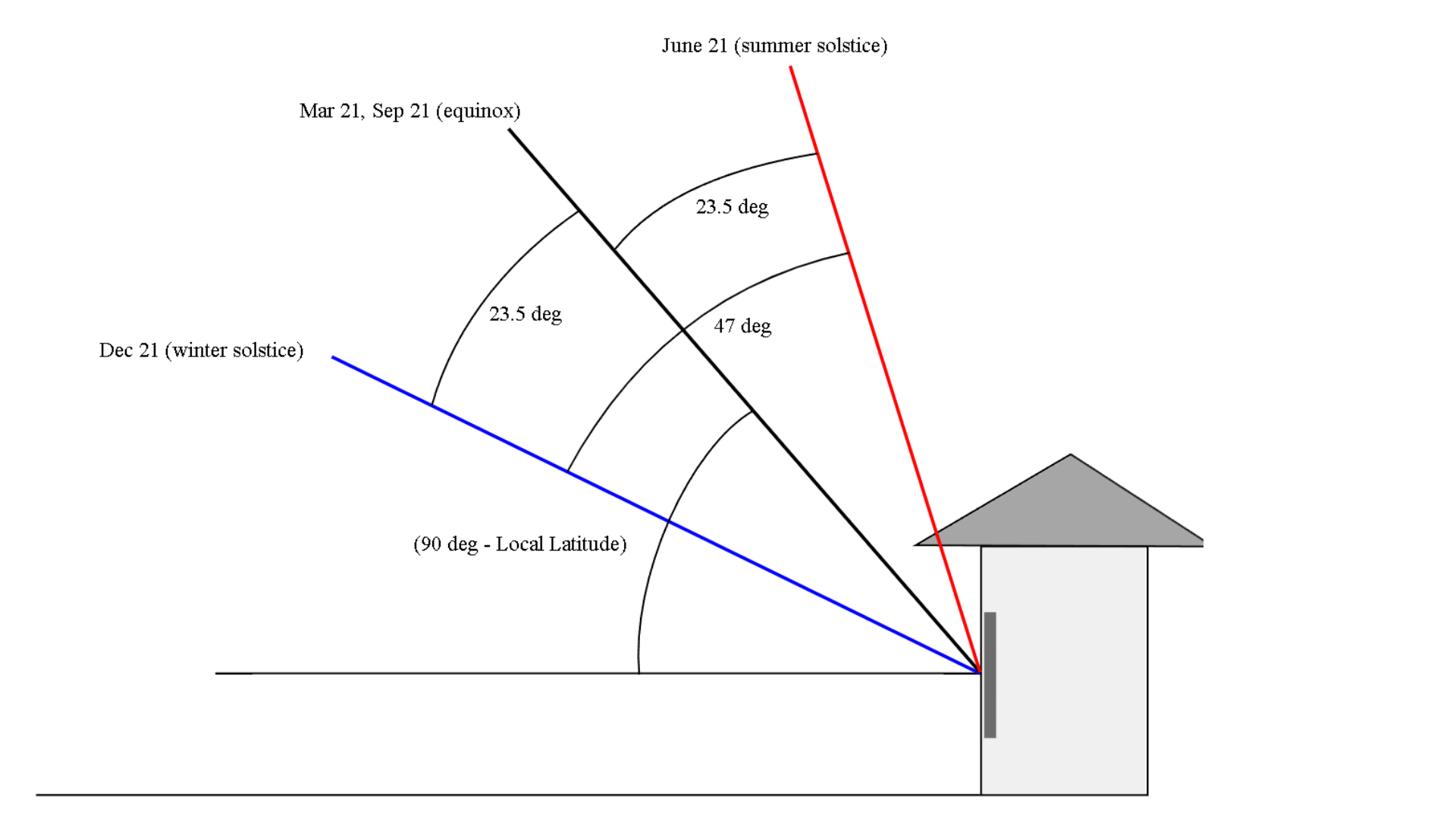
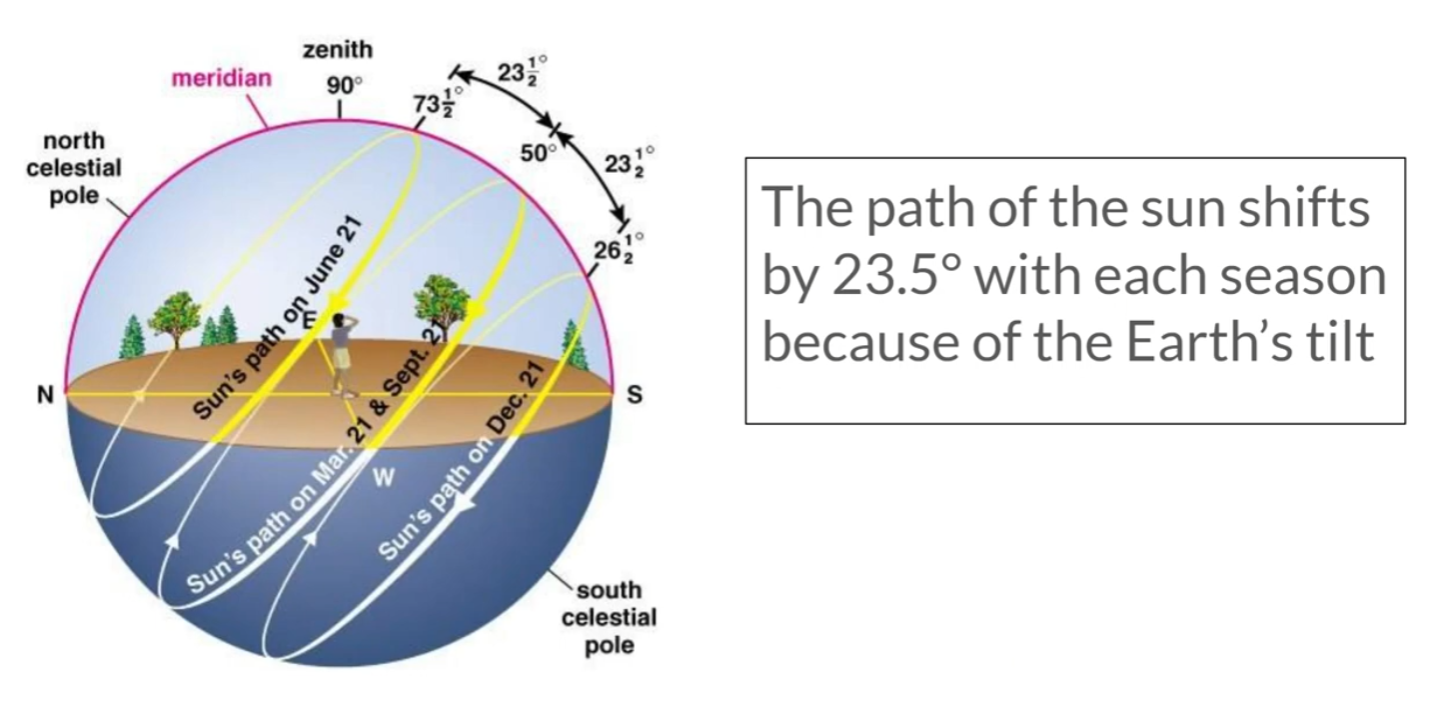
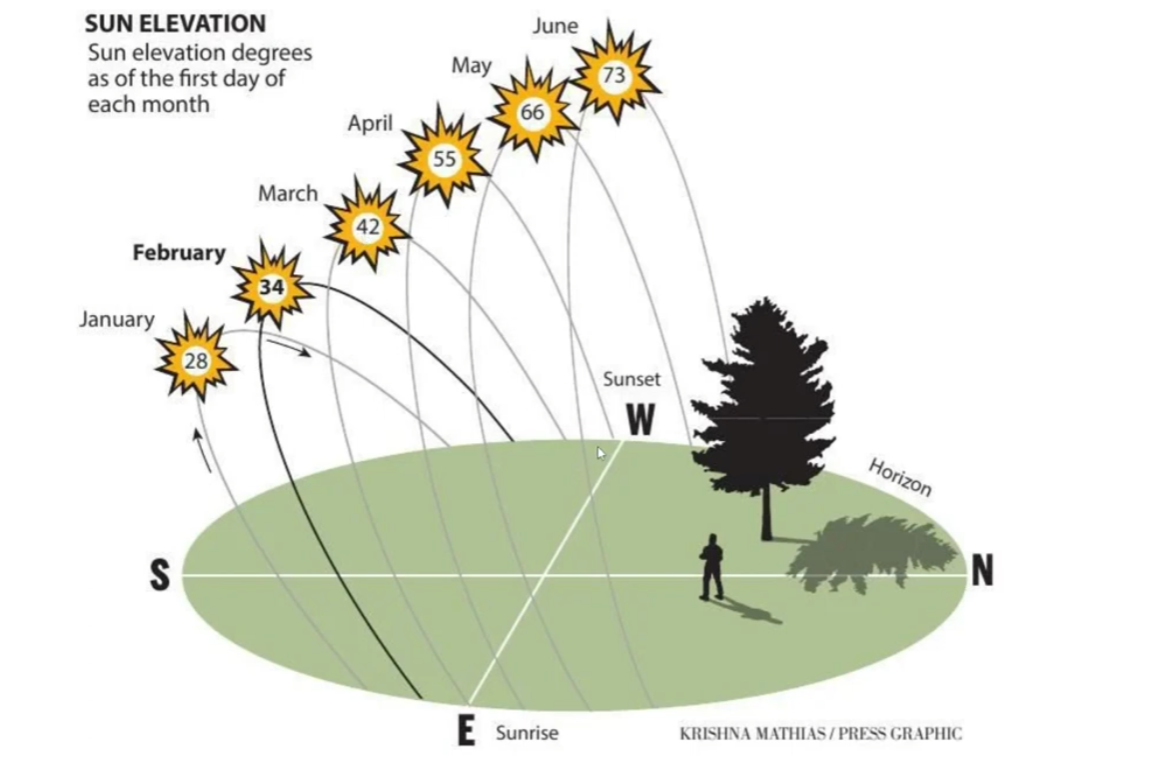
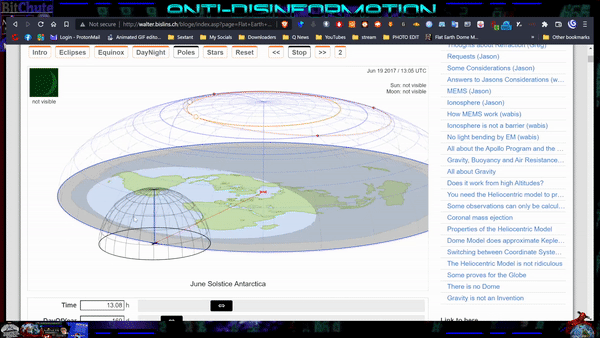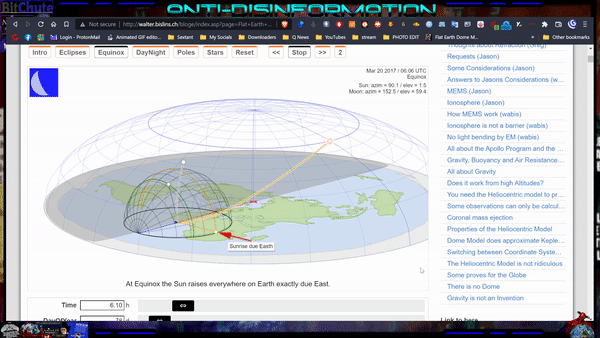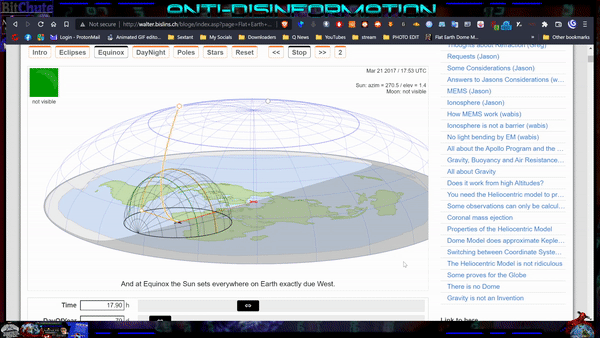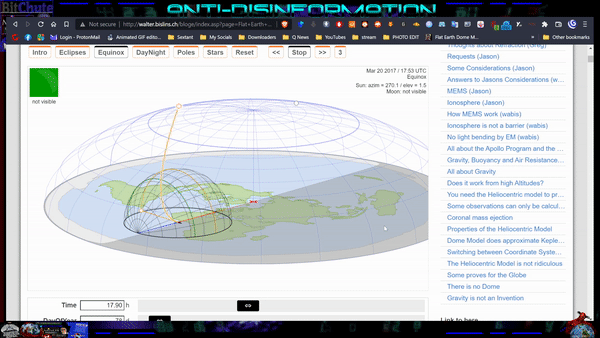
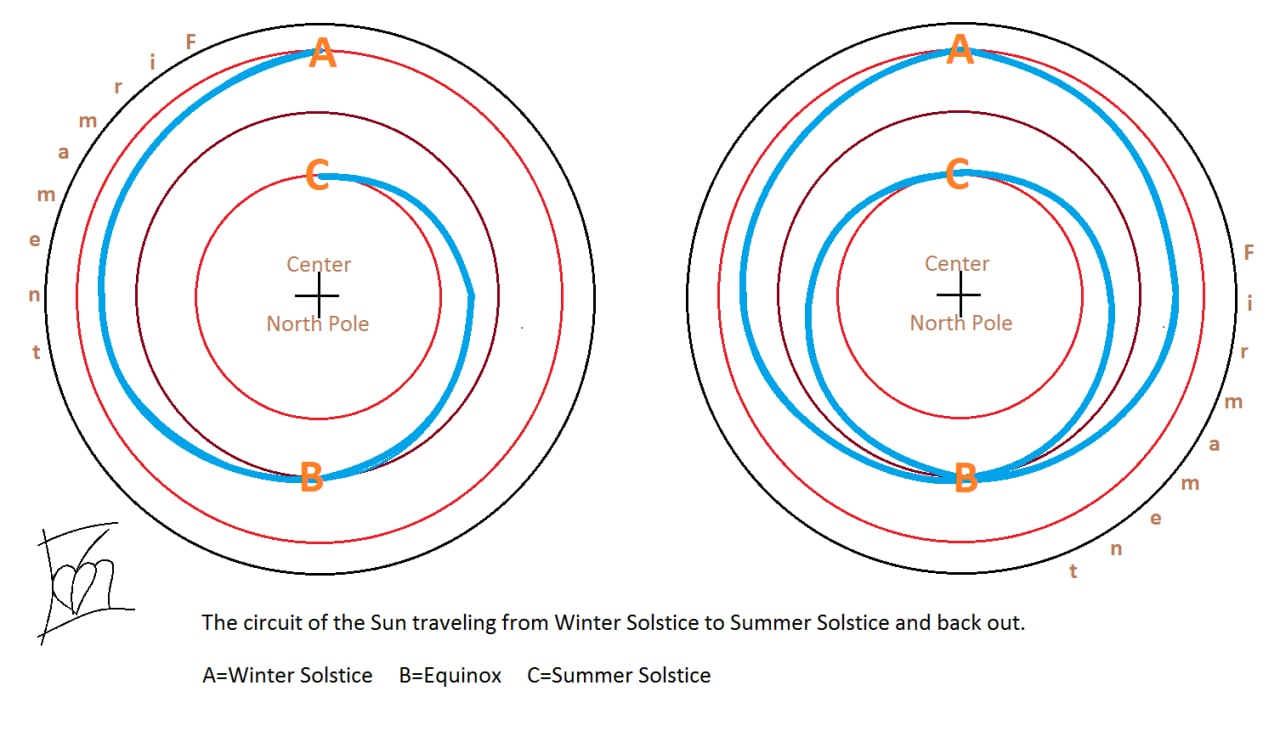
The Earth is as a flat plane, with the North Pole at its center and the boundaries defined by the continent of Antarctica. The sun revolves around the Earth in a defined, limited and cyclical journey.
During the Earth's "summer" in the northern hemisphere, the sun moves closer to the Tropic of Cancer, which marks the farthest point north where the sun's rays reach. As it journeys through the tropical gap, the sun illuminates the northern hemisphere, casting its light and creating daylight for that part of the world. The days are longer, and the warmth of the sun is felt more intensely in these regions.
After reaching the Tropic of Cancer, the sun begins its gradual movement southward, crossing the equator and heading toward the Tropic of Capricorn. As it progresses, the sun's rays cover the southern hemisphere, but not beyond 70degrees parallel south, bringing light and warmth to those regions while the northern hemisphere experiences shorter days and cooler temperatures.
Once the sun reaches the Tropic of Capricorn, it starts its journey back toward the equator, within the tropical gap once again. This continuous cycle of the sun's limited journey creates the familiar patterns of day and night, as well as the changing seasons experienced on the Earth.
Due to the restricted reach of the sun's rays, only half of the Earth is illuminated at any given time. The other half remains in darkness, resulting in the cycle of day and night as the Sun moves over the Earth. This limited coverage of sunlight creates the variation in seasons as the Sun revolves around the Earth throughout the year.

Tangential Velocity
]
]




[http://www.jgiesen.de/Divers/Sonnenuhr/Sonnenuhr.html](http://www.jgiesen.de/Divers/Sonnenuhr/Sonnenuhr.html)
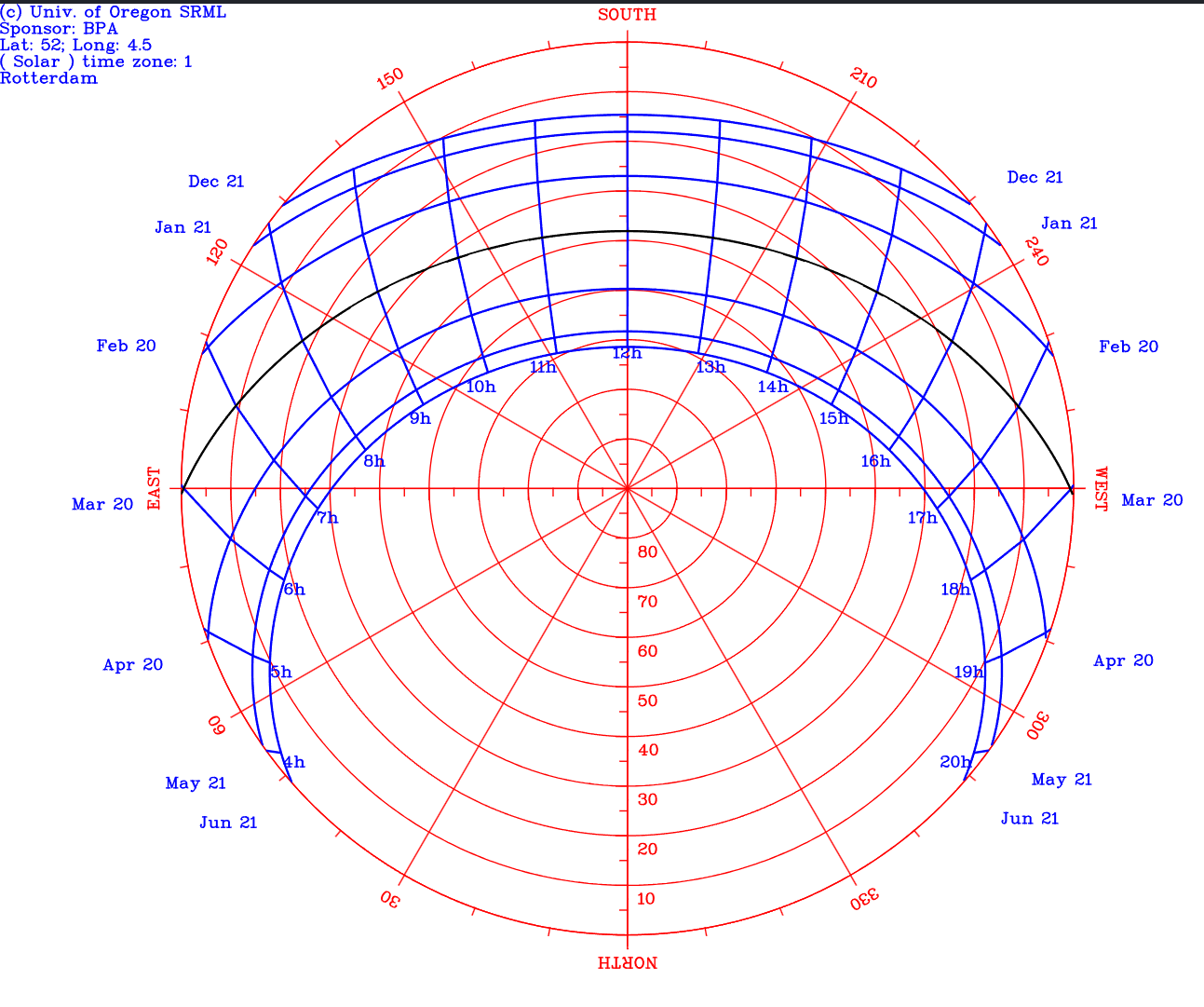
[http://www.jgiesen.de/map/index.html](http://www.jgiesen.de/map/index.html)
## Sunsets
.gif)


## Fade outs
.gif)
##### The green flash
I Put this globe video here, because without the spherical limit of vision, I would like a



%201.gif)

%202%201%201%201%201%201%201%201.jpg)
## Fade In
]
.gif)

## Can we see infinitely?
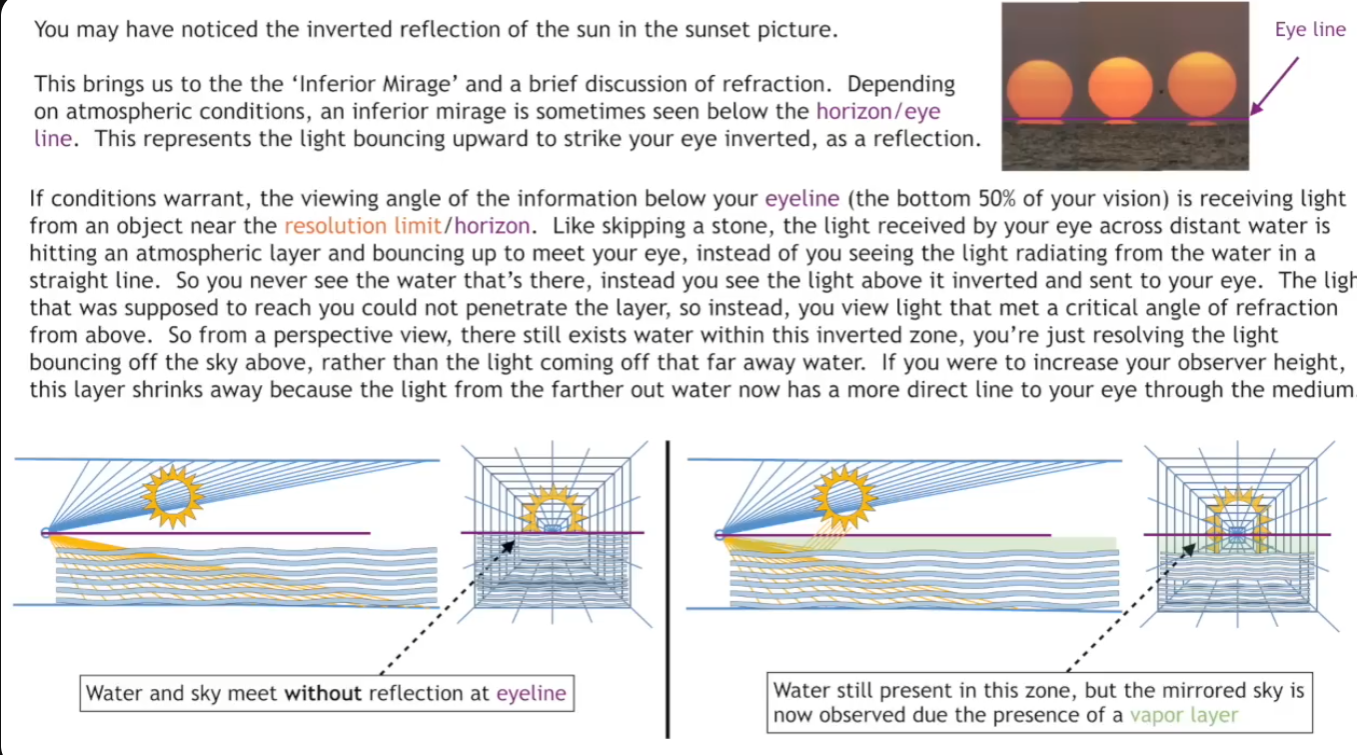

## Perspective
the sun and moon set due to angular resolution and the limits of human vision. It suggests that the sun and moon do not change in size as they set, but rather travel in a straight line across a flat plane until they reach the vanishing point of our perspective, at which point they "set" or disappear from view.



.gif)

.gif)

## Toroidal SUn, Toroidal Earth
Flat Earth - ABSOLUTE MUST SEE!
[https://www.youtube.com/watch?v=nPlNcJ_IC5w&ab_channel=Steve](https://www.youtube.com/watch?v=nPlNcJ_IC5w&ab_channel=Steve)
Flat Earth Magnetic Sun


%201.gif)

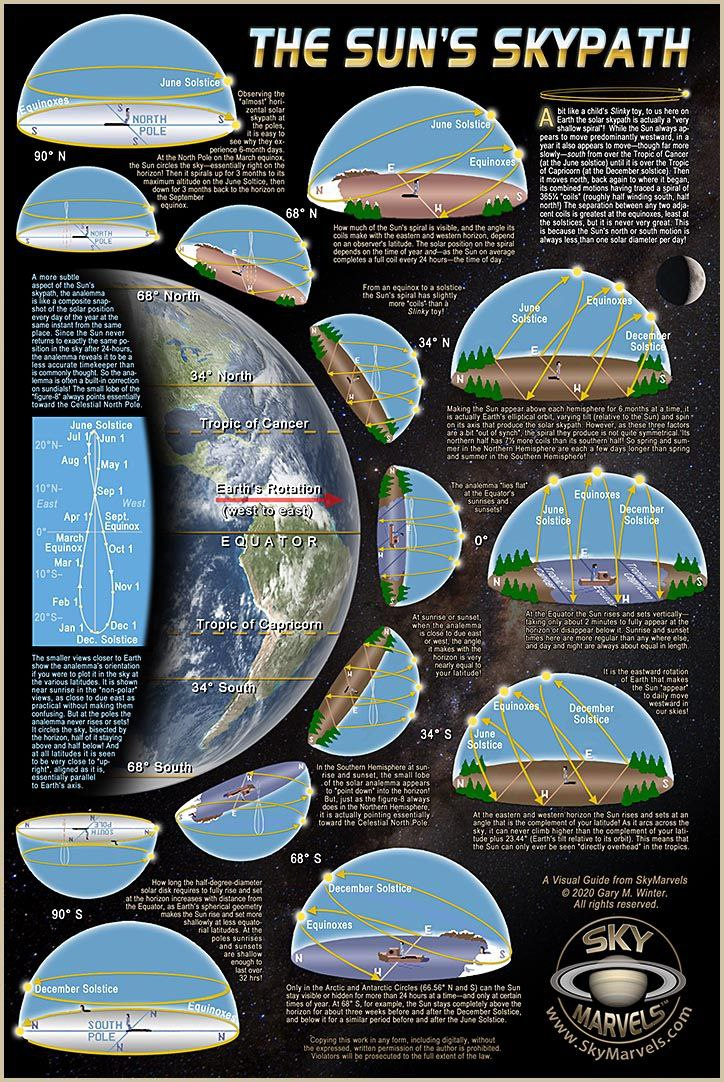
This [solargraph](https://en.wikipedia.org/wiki/Solarigraphy) exposed over the course of a year shows the Sun's paths of [diurnal motion](https://en.wikipedia.org/wiki/Diurnal_motion "Diurnal motion"), as seen from [Budapest](https://en.wikipedia.org/wiki/Budapest "Budapest") in 2014.

Pinhole Camera on the sun
.gif)
[http://www.jgiesen.de/planets/index.html](http://www.jgiesen.de/planets/index.html)
[http://www.jgiesen.de/hsd/hsd300.html](http://www.jgiesen.de/hsd/hsd300.html)
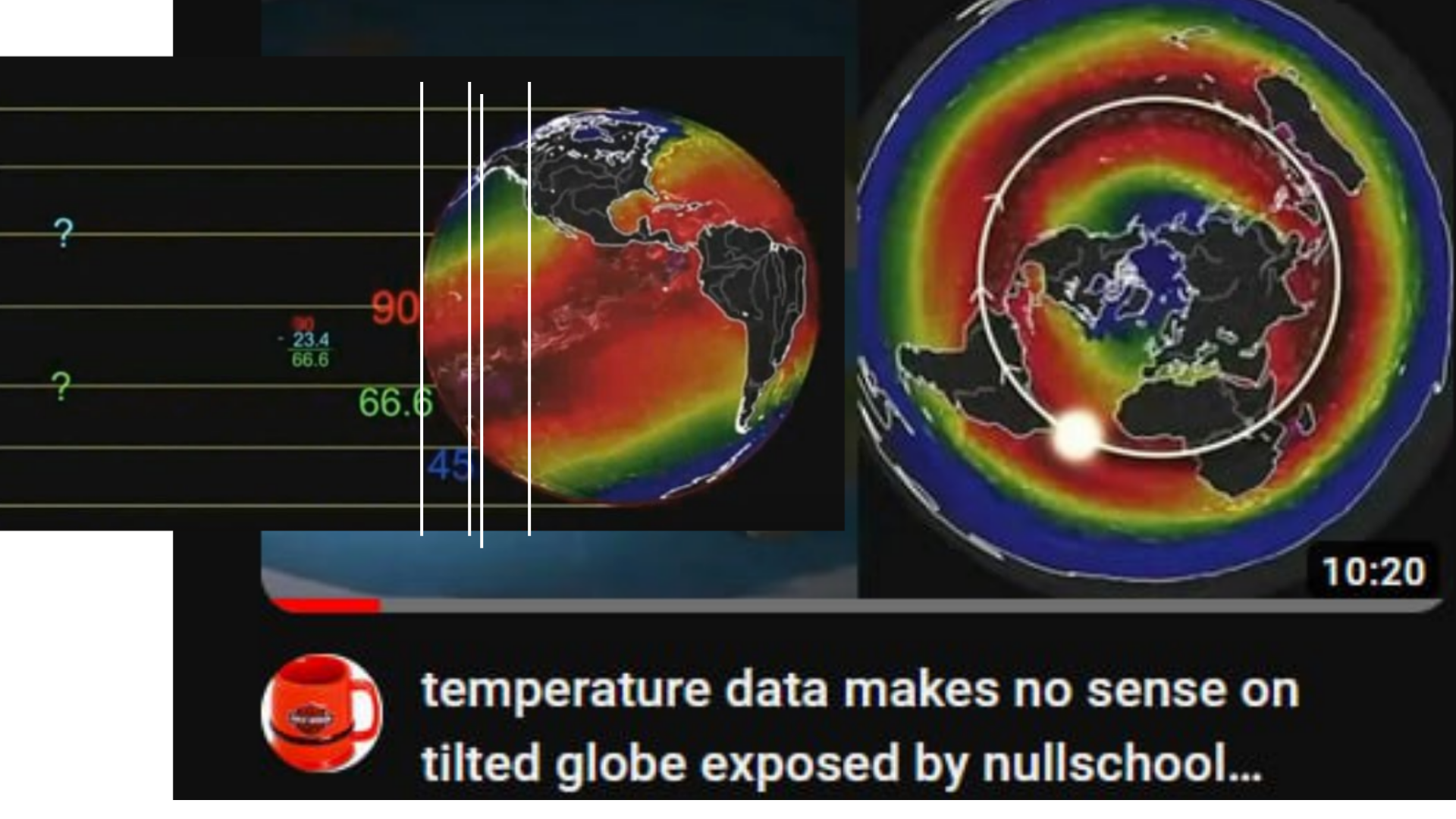
## Spherical Limit of Vision


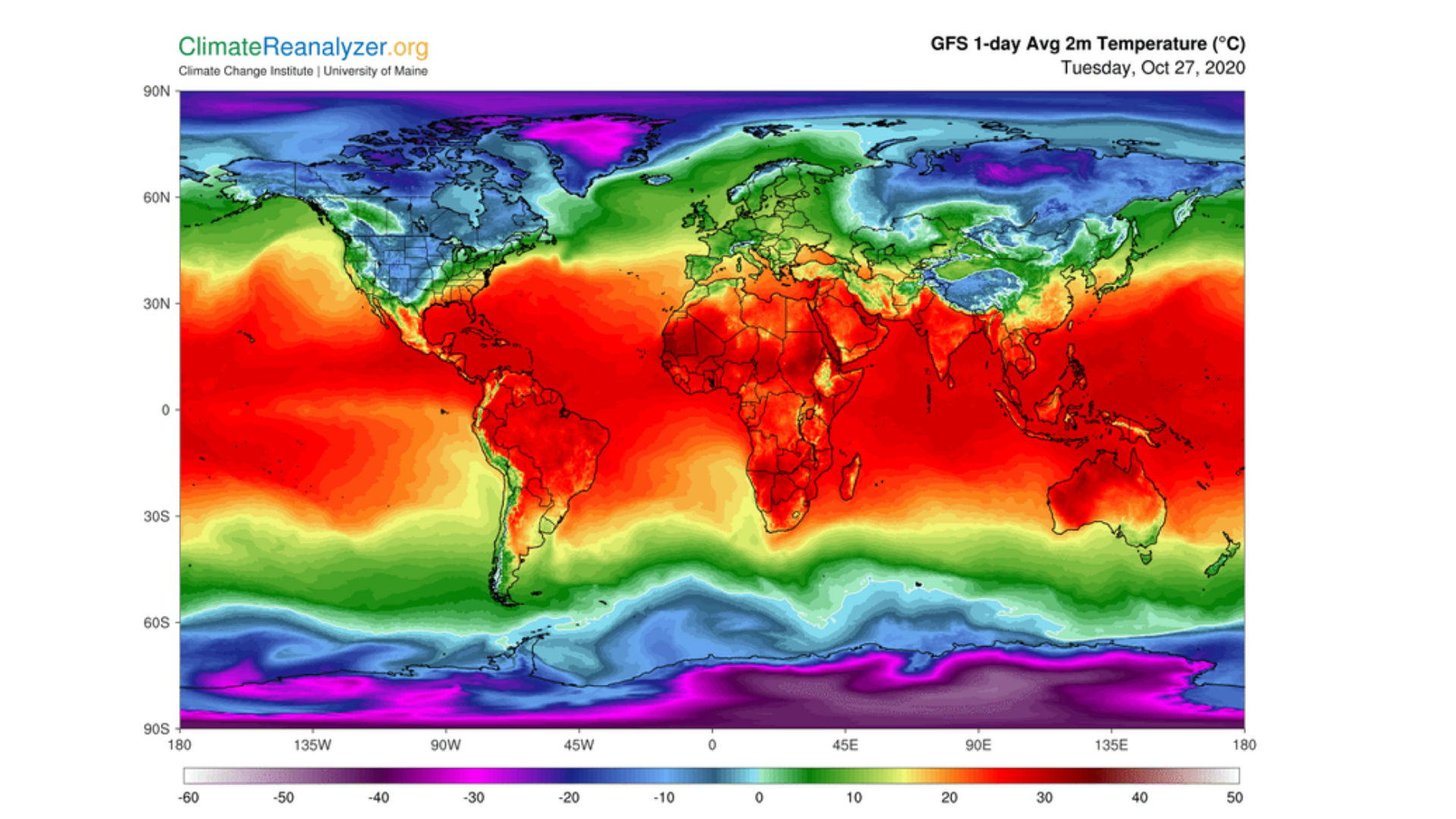
### Heat Distribution on Earth
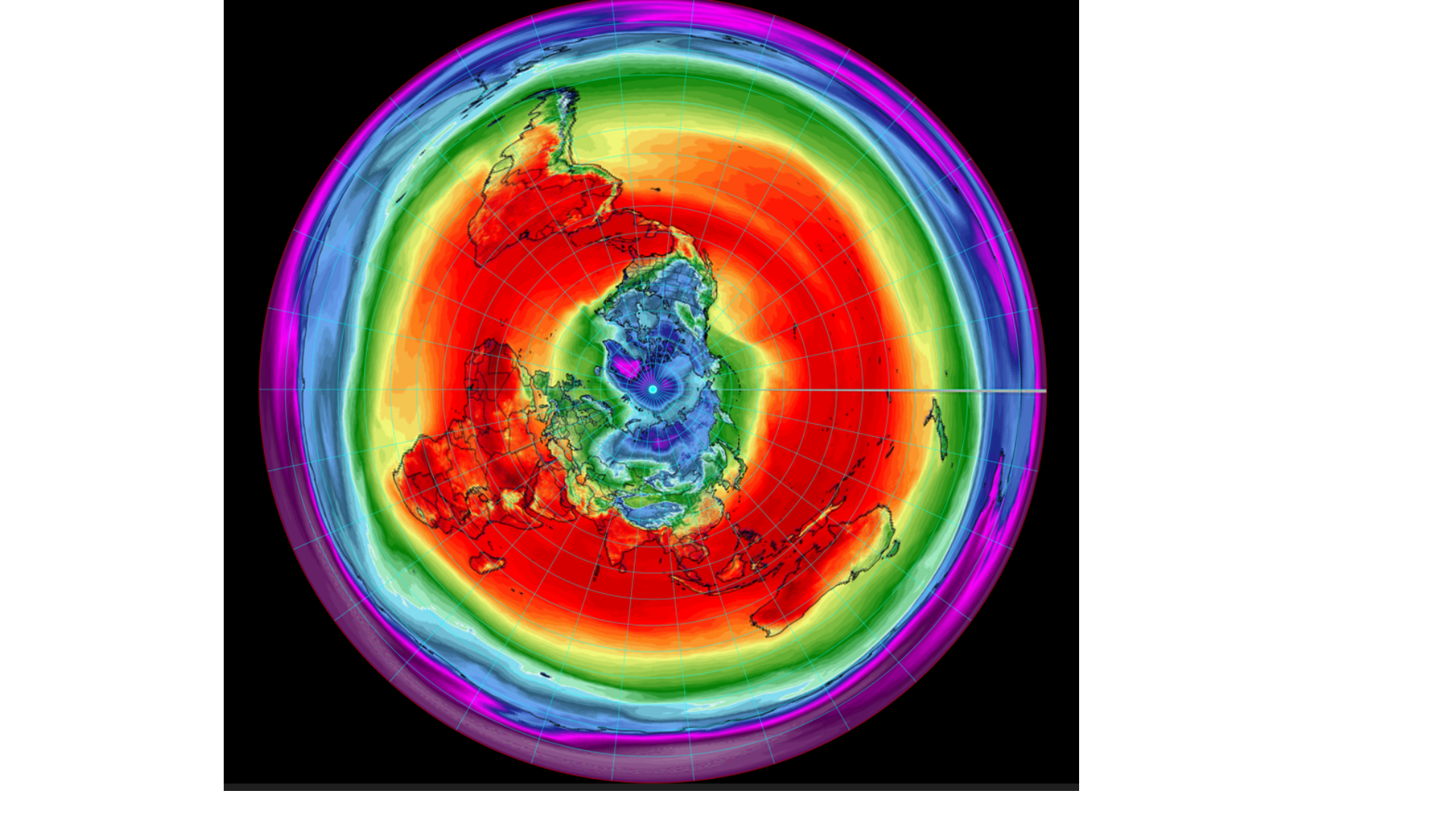





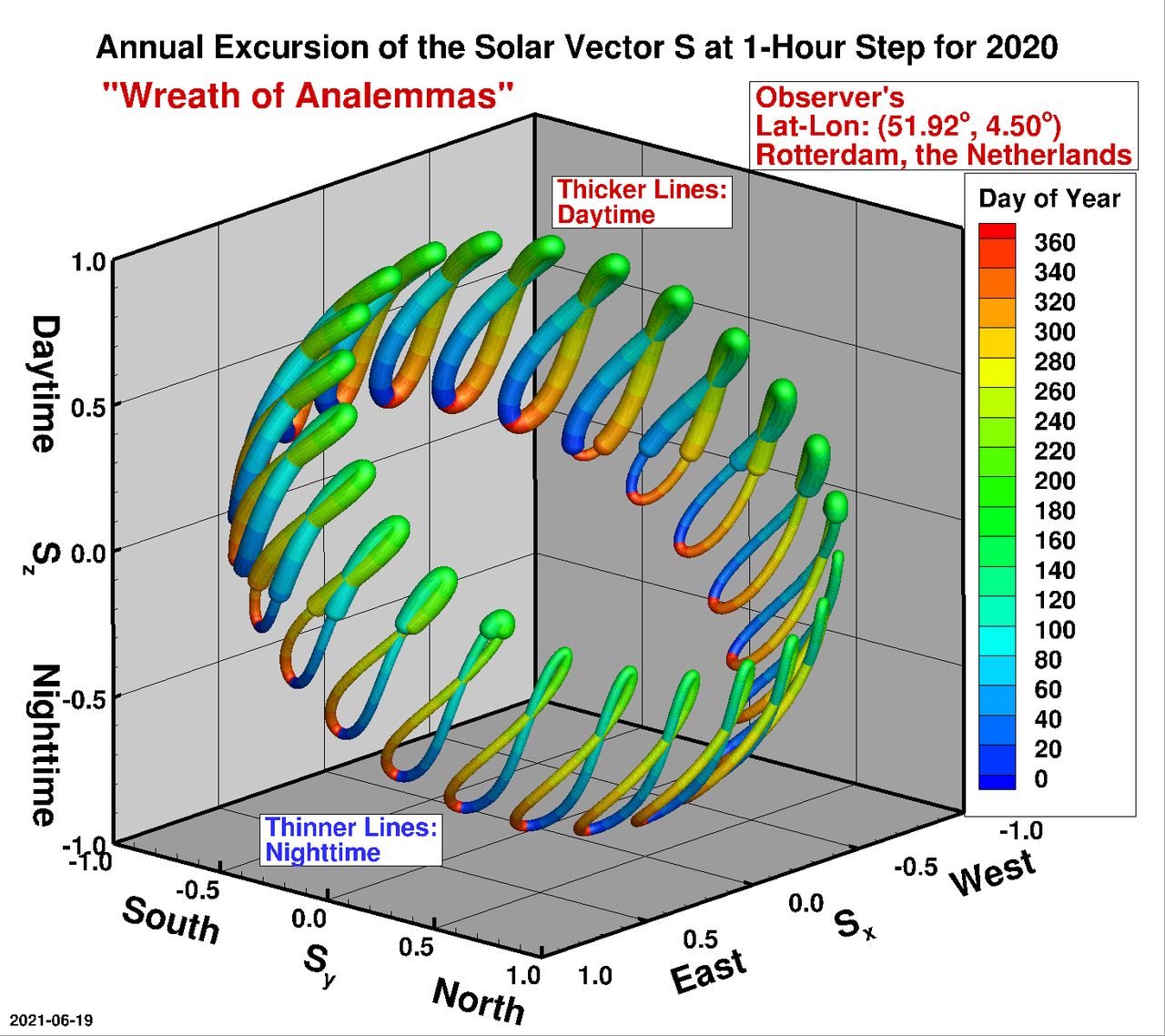
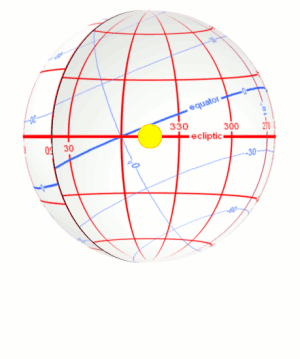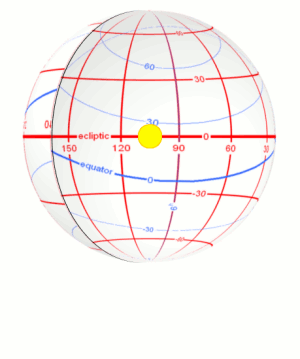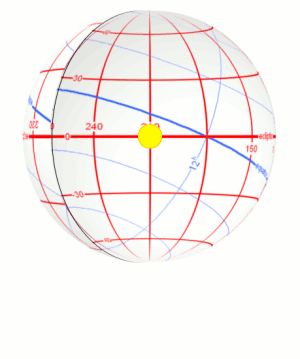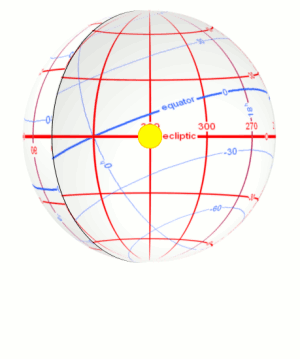
## Analemma
[http://www.jgiesen.de/Divers/Sonnenuhr/Sonnenuhr.html](http://www.jgiesen.de/Divers/Sonnenuhr/Sonnenuhr.html)


# The Moon

ThE moon
As the moon revolves around the earth in twenty nine and one-half days, the twelve months of the year must alternately possess thirty and twenty-nine days in order to keep up her movements—twelve lunations or months (Moon-eths,) in a year. This is a system now followed by the Jews, Turks and Chinese, w ho use the original Lunar Year, the months of which are more astronomical than our Pagan, Solar year, which, although a perfect measure of time, can begin and end anywhere, and have months of irregular length. The Lunar year, and each month of the year, must begin with a new moon.




## Scaling Invariance













[http://www.jgiesen.de/planets/index.html](http://www.jgiesen.de/planets/index.html)
[http://www.jgiesen.de/hsd/hsd300.html](http://www.jgiesen.de/hsd/hsd300.html)
## Good ole Rory
Rory's single talking point:
**Step 1:** Pick your favorite continent, but make sure it's one that you think has either been accurately measured/mapped or pick one where you think long distances on it can be easily and accurately estimated.
**Step 2:** Pick either the Equator, the Tropic of Cancer, or the Tropic of Capricorn, whichever one runs through your chosen continent.
**Step 3:** Find the approximate points where the Tropic/Equator meets the East and West coast of that continent.
**Step 4:** Find the approximate distance between those two points. The nearest 10 kilometers or miles will do, but the more accurate, the better. Use whatever maps, programs, or data that you think most accurately represents reality and provide them so we can use the same info to compare results and determine the level of accuracy.
**Step 5:** Figure out the approximate times when the Sun appears to be directly over those two points on the appropriate Solstice or an Equinox. Use the December Solstice for the Tropic of Capricorn, the June Solstice for the Tropic of Cancer, or an Equinox for the Equator. There are resources that provide those times based on the position to the nearest minute or even the nearest second.
**Step 6:** Calculate the amount of time it took the Sun to trace from directly over the East coast to directly over the West coast to around the nearest minute or hundredth of an hour.
**Step 7:** Take your distance, divide it by your time, and then multiply it by 24 so you get the approximate length of the total path that the Sun traced over after 24 hours. This will be your estimated length of a Tropic or the Equator.
**Step 8:** Repeat steps 1-7 with other continents and other Tropics or the Equator. Perhaps you'll get results that show the Tropic of Capricorn to be twice the length that it's accepted to be on a globe and finally disprove a spherical Earth once and for all.
As an example, I tried this with Australia on the December Solstice. It took the Sun about 2.47 hours to trace from one shore to the other. The distance was about 3786km. That means my estimate for the length of the Tropic of Capricorn would be just over 36787km long which is less than a kilometer from the accepted length on a globe. If I go through these steps again with South America on an Equinox then I can check the estimated length of the Equator. The sun appeared to trace over 3423km in 2.05 hours which would make the Equator approximately 40074km long. Again, I'm only one km off from the accepted length on a globe. If I repeat it again with Africa on the June Solstice, I get an approximate length for the Equator of 36819km which is around 31km longer than the accepted length on a globe. That's still over 99.9% accurate to the accepted length on a globe. Precisely no pair of these lengths sync up to a Gleason map.
Whenever I use an accurate resource like Time and Date's Sunrise and Sunset Calculator or the NOAA Solar Calculator to get the local solar noon times and something like Google Earth or any other accurate mapping program to get the distance between the two shore points on any continent, I always get results that are within 99.9% of a percent from the accepted length on a globe.
Notice step 4: Go grab your favorite globe distance. This is the part where the entire argument breaks down. There is only the globe distance. We are only ever given distance X, and our only means to verify it, trigonometry from the sky, will always confirm the same. This is the basis, and the backbone of the globe model. The fact that he has never addressed this is the entire issue. Anyway, we continue:

### Why it doesn't prove anything:
I have long been arguing the distances based on the graticule do not prove anything. They only prove that the globe model is based on the celestial sphere. The entire map argument does not prove the shape of the earth either way, and I have the sources to prove it. (And an open challenge to the internet to debate anyone who thinks they can prove maps prove the earth is a globe). Now, on to his 'method' of comparing geographic graticule distances to the globe mode.
His argument is essentially a dressed-up attack at our lack of a map. End of story. We know calculated distances match the globe. It was my premise; how can it be his conclusion? 😂
**His argument is essentially a dressed up attack at our lack of a map.**
The method uses distances based on the graticule (the system of latitude and longitude) because these measurements are derived from astronomical observations of the stars and celestial bodies. The graticule is a framework used to map the Earth's surface using angular coordinates, which are calculated based on the rotation of the celestial and your position relative to the stars.
The accuracy of the graticule is well-established in spherical Earth models, where the distances between points (like along the Equator or Tropics) can be calculated with high precision. These calculations are the backbone of the globe model. Eratosthenes himself used similar measurements to calculate an identical circumference, which was also incorrectly applied to a spherical earth instead of a circular limit.
These calculations are consistent with measurements made using various methods, including modern technology like GPS, which also heavily relies on coordinate systems and the graticule.
Nautical miles are consistent across different coordinate systems, whether using the celestial sphere or the geographic graticule. This consistency is crucial because it ensures that distances measured remain the same regardless of the Earth's shape. The use of nautical miles allows for uniformity in measurements, whether navigating by the stars or using Earth's coordinates. This consistency helps reify the spherical model of the Earth, as the distances remain accurate and meaningful in both contexts.
### For example:
Note on the above*
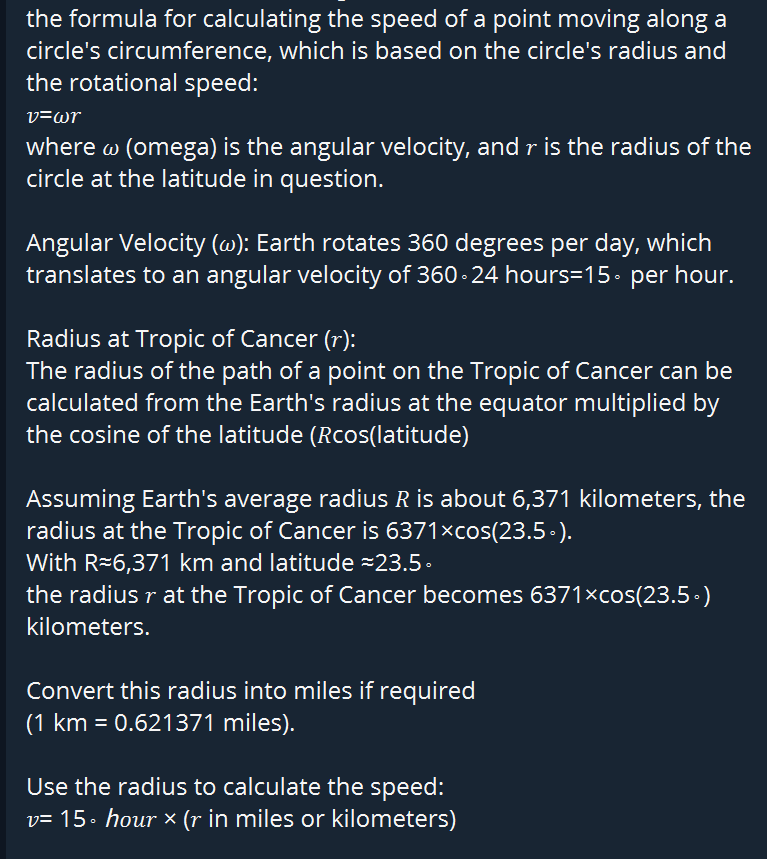
ALL distances based on the graticule. the formula for calculating the speed of a point moving along a circle's circumference, which is based on the circle's radius and the rotational speed:
𝑣=𝜔𝑟
where 𝜔 (omega) is the angular velocity,
and 𝑟 is the radius of the circle at the latitude in question.
Angular Velocity (𝜔):
Earth rotates 360 degrees per day, which translates to an angular velocity of 360∘24 hours=15∘ per hour.
The radius of the path of a point on the Tropic of Cancer can be calculated from the Earth's radius at the equator multiplied by the cosine of the latitude (𝑅cos(latitude)
Assuming Earth's average radius 𝑅 is about 6,371 kilometers,
the radius at the Tropic of Cancer is 6371×cos(23.5∘).
With R≈6,371 km and latitude ≈23.5∘ the radius 𝑟 at the Tropic of Cancer becomes 6371×cos(23.5∘) kilometers.
Convert this radius into miles if required (1 km = 0.621371 miles).
Use the radius to calculate the speed: 𝑣= 15∘ ℎ𝑜𝑢𝑟 × (𝑟 in miles or kilometers)
At the equator, the distance per degree of longitude is about 69 miles (or about 111 kilometers). This is derived by dividing the Earth's equatorial circumference by 360 degrees. The formula to calculate the actual distance per degree of longitude at a given latitude is: 𝐷=cos(latitude)×69 miles
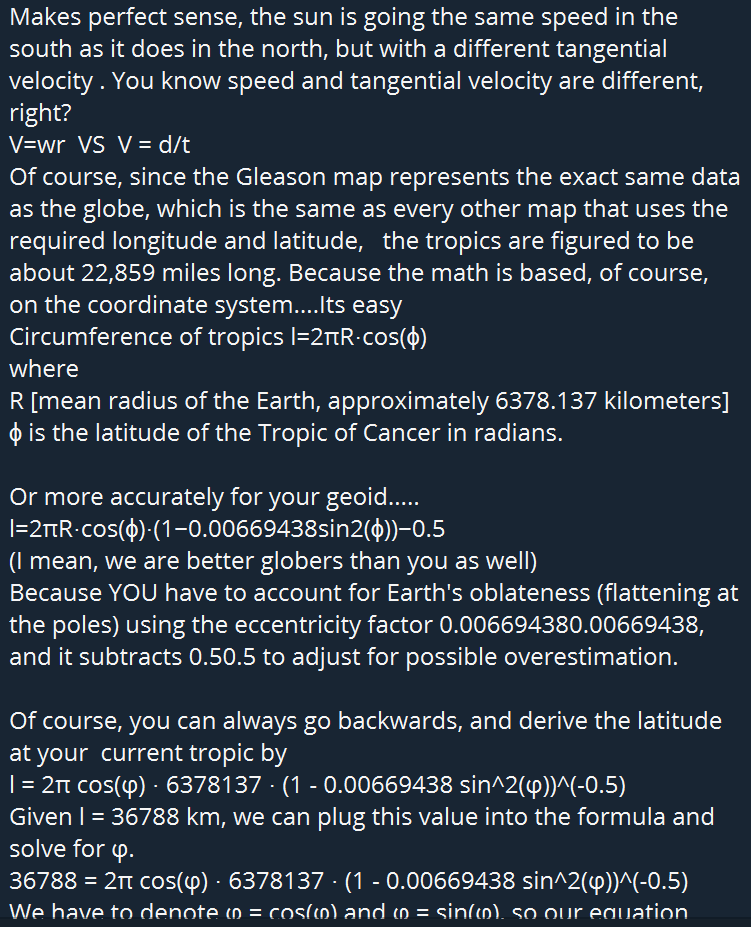
the sun is going the same speed in the south as it does in the north, but with a different tangential velocity. Speed and tangential velocity are different:
Speed
V=wr
VS
tangential velocity
V = d/t
Of course, since the Gleason map represents the exact same data as the globe, which is the same as every other map that uses the required longitude and latitude, the tropics are figured to be about 22,859 miles long. Because the math is based, of course, on the coordinate system....Its easy
Circumference of tropics l=2πR⋅cos(ϕ)
where
R [mean radius of the Earth, approximately 6378.137 kilometers]
ϕ is the latitude of the Tropic of Cancer in radians.
Or more accurately for your geoid.....
l=2πR⋅cos(ϕ)⋅(1−0.00669438sin2(ϕ))−0.5
(I mean, we are better globers than you as well)
Because YOU have to account for Earth's oblateness (flattening at the poles) using the eccentricity factor 0.006694380.00669438, and it subtracts 0.50.5 to adjust for possible overestimation.

### Upward Shadow
https://youtu.be/bIn6nEMEy1s?si=9_BNdhVlGcZi2LHf