By Alexandra Veremeychik and Rebin Muhammad On Saturday, November 16th, Montgomery College held its annual [SK Day](https://www.montgomerycollege.edu/academics/stem-and-health-sciences/k-12/sonya-kovalevsky-program.html), named after Sofya Kovalevskaya, the first woman to receive a modern doctorate.  The objective of the program is to host middle school students and spark in them an adventurous curiosity in the sciences. This includes facilitating enriching activities that turned participants into chemists, data scientists, and mathematicians. The theme of the math adventure was graph theory, titled “Graph Colorama: Finding the Chromatic Number.” in which I was a co-facilitator.   The activity began with a discussion of the word “graph” and what it means to the budding theorists. In addition to being asked for the definition, the participants were encouraged to come up to the board and draw an example of a graph. This yielded a colorful variety of line graphs, scatterplots, pie charts, and bar graphs. Clearly their school curriculum leading up to this point had exposed them to several graph variations and offered them opportunities to create their own.  Once each group had come to a consensus on what the general concept of a graph entails, they were promptly and emphatically encouraged to forget it. At least for the remainder of the activity. A simple cycle graph consisting of three vertices was then drawn on the board. The young mathematicians were informed that this was an example of the new face we were putting on the word “graph”. They were prompted to share ideas for what to name the circles, for which they came up with a selection of words (most notably one group wanted to name them “bobs”), and for the lines as well. Once the real names for these objects were revealed to be vertices and edges, respectively, the rules for what constitutes such a graph were explained. Knowing that no two vertices were required to be connected by edges, but that each edge had to connect exactly two vertices, the fledgling mathematicians were ready to begin creating graphs of their own.  The adventure then continued at the whiteboard. With dry erase markers already positioned around the room’s three covered walls, everyone was encouraged to get up and draw whatever graph they wanted, as long as it satisfied the rules we put forth in our definition. The childrens’ various tastes, strengths, and personalities were on display in the variety of shapes their graphs took. After all of the boards were covered in diagrams, the participants were introduced to the idea of coloring in the vertices, allowing them to fill their creations using the selection of markers. Following this explosion of color, they returned to their seats and began coming up with some coloring rules in order to make the process more game-like. The rule settled on was one that prohibited two connected vertices from being the same color.  In order to play with these new rules, the class was then invited to pick up their designated Ipads which were provided by the Mathematics Department at Rockville Campus In Montgomery College. Opened and bookmarked on each device was [Graph Colorama](https://reben80.github.io/chromatic-number-new-/). This app was created especially for participants of this chromatic number activity. It allows users to color in graphs using these very rules. The game consists of three modes.   The first takes a number entered by the user and generates a random graph with that number of vertices and a random set of edges.  The user then must try to color in the generated graph. The app prohibits the coloring of two connected vertices and informs the player that they are breaking a rule when they attempt to do so.  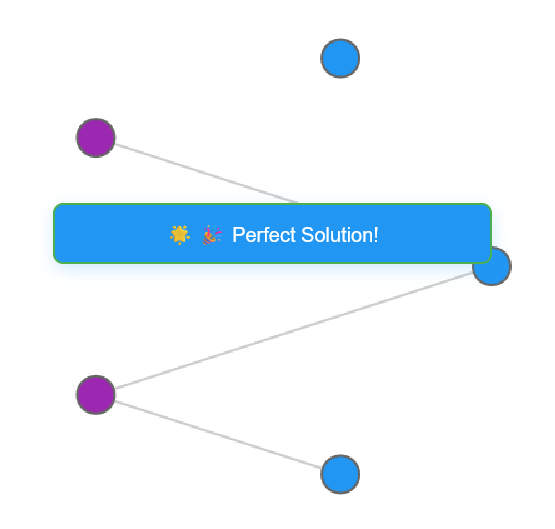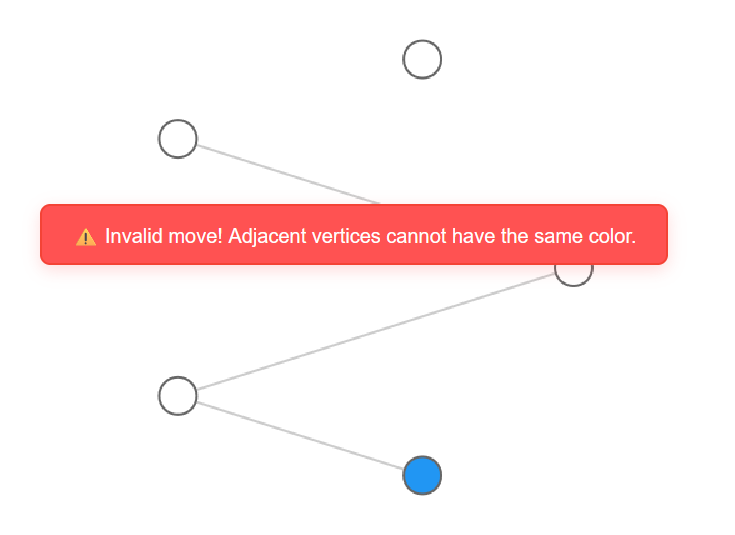The second mode sets forth eight challenges, with one initially unlocked, and the rest getting progressively unlocked as more are completed. A challenge is deemed completed when every vertex is colored by using the smallest set of colors possible. In other words, the challenge is to find each graph’s chromatic number.  The result of completing a graph is a short message popping up. It reads “Can you do better?” if the player uses more colors that is the number deemed by the game to be the chromatic number. A chromatic number is the minimum number of colors needed to color a graph's vertices so that no adjacent vertices have the same color. 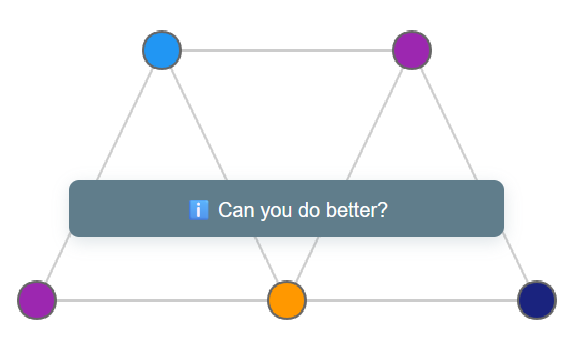 Once the player has colored in a particular graph using the chromatic number of colors, another short message pops up reading “Perfect solution!”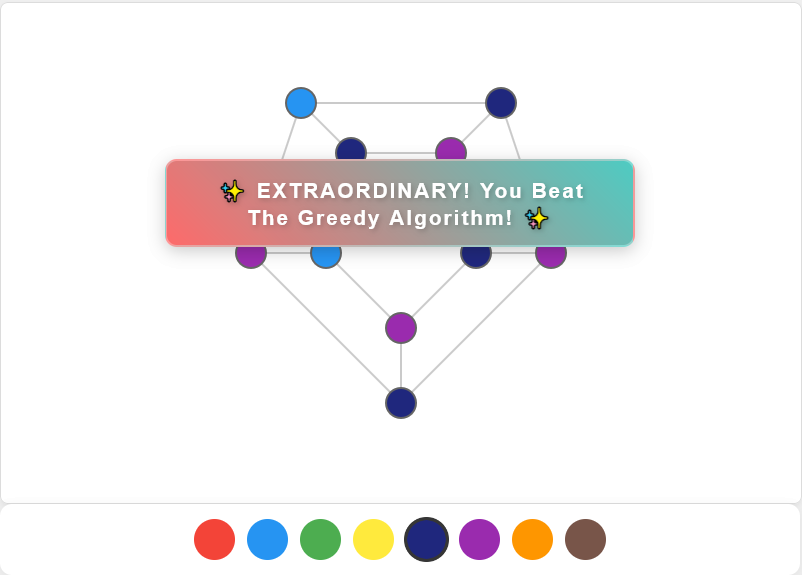 A perfect solution is sufficient to move on to the next level of challenges based on Greedy Algorithm for coloring graphs, however there is one more pop up that players can encounter. The message on it reads “EXTRAORDINARY! You beat the greedy algorithm!” A “greedy” algorithm is one that selects the best choice at any given position, regardless of past information. So when it is tasked with coloring in a graph, this method goes from vertex to vertex, filling each in according to a set order. When it encounters a vertex with edges touching other vertices, it changes the color and moves on. At times this will result in the algorithm overestimating the chromatic number, allowing us humans a chance to do better. Participants were encouraged to play with both of these modes as they wished, but prompted to complete all eight challenges at some point, as reaching Challenge 8 offers a guaranteed opportunity to beat the algorithm which almost most of them found. The third mode included in the game is the sketch mode. With sketch mode the player is able to create their own graphs by plotting vertices and connecting them with edges as they wish. Then those very graphs can be colored in. This is another mode that has the capacity to allow for beating the greedy algorithm. The children’s creativity once again was displayed vibrantly in the graphs they came up with in this mode. They all created graphs with different shapes, numbers of vertices and edges. Many of the mathematicians took to the suggestion of creating challenges for others with great joy. They created a variety of graphs and then passed them to their friends to color in. Some even challenged the leaders of the activity to fill out their graphs. In some cases, their creations provided another opportunity to beat the greedy algorithm. The final problem presented to the graph theorists was to come up with a graph that had a chromatic number of eight (the total number of colors available) and only 8 vertices. In each group, a portion were able to successfully figure out the trick to achieving the objective: making sure every vertex in the graph was connected to every other vertex in the graph. This led to the perfect opportunity to learn that such a graph is known as a “complete graph”. It should not be understated how difficult it can be to conceptualize graph theory enough to not only create a complete graph, but to be able to explain what makes it complete. As facilitators of this journey, this was possibly our proudest moment. To conclude the vibrant experience, the intellectual explorers were encouraged to envision themselves to be vertices. They were then “colored in” with vibrant hats that they could then take home with them as a reminder of all the graphs they colored in. With hats on heads they received one final token of the journey - a pocket full of additional challenges to complete at their own leisure. The packet, which can be found [here](https://github.com/Reben80/Graph_Coloring/blob/main/Chromatic_Number-3.pdf), also included a QR code to the [Graph Colorama](https://reben80.github.io/chromatic-number-new-/) app. Many of the participants went home with plans to challenge their friends and family to their own graph coloring adventure. Curiosity sparked.**